Introduction to NumPy¶

Peer Herholz (he/him)
Postdoctoral researcher - NeuroDataScience lab at MNI/McGill, UNIQUE
Member - BIDS, ReproNim, Brainhack, Neuromod, OHBM SEA-SIG

@peerherholz

Disclaimer: Most of the content in this notebook is coming from www.scipy-lectures.org

NumPy¶

NumPy is the fundamental package for scientific computing with Python. It is the basic building block of most data analysis in Python and contains highly optimized routines for creating and manipulating arrays.

Everything revolves around numpy arrays¶

Scipy adds a bunch of useful science and engineering routines that operate on numpy arrays. E.g. signal processing, statistical distributions, image analysis, etc.
pandas adds powerful methods for manipulating numpy arrays. Like data frames in R - but typically faster.
scikit-learn supports state-of-the-art machine learning over numpy arrays. Inputs and outputs of virtually all functions are numpy arrays.
If you want many more short exercises than the ones in this notebook - you can find 100 of them here

NumPy arrays vs Python arrays¶

NumPy arrays look very similar to Pyhon arrays.

import numpy as np
a = np.array([0, 1, 2, 3])
a

So, why is this useful? NumPy arrays are memory-efficient containers that provide fast numerical operations. We can show this very quickly by running a simple computation on the same two arrays.

L = range(1000)

# Computing the power of the first 1000 numbers with Python arrays
%timeit [i**2 for i in L]

a = np.array(L)

# Computing the power of the first 1000 numbers with Numpy arrays
%timeit a**2

Creating arrays¶

Manual construction of arrays¶

You can create NumPy arrays manually almost in the same way as in Python in general.

1-D¶

a = np.array([0, 1, 2, 3])
a

a.shape

2-D, 3-D, …¶

b = np.array([[0, 1, 2], [3, 4, 5]])    # 2 x 3 array
b

b.shape

c = np.array([[[1], [2]], [[3], [4]]])
c

c.shape

Functions for creating arrays¶

In practice, we rarely enter items one by one. Therefore, NumPy offers many different helper functions.

Evenly spaced¶

a = np.arange(10) # 0 .. n-1  (!)
a

b = np.arange(1, 9, 2) # start, end (exclusive), step
b

… or by number of points¶

c = np.linspace(0, 1, 6)   # start, end, num-points
c

d = np.linspace(0, 1, 5, endpoint=False)
d

Common arrays¶

a = np.ones((3, 3))  # reminder: (3, 3) is a tuple
a

b = np.zeros((2, 2))
b

c = np.eye(3)
c

d = np.diag(np.array([1, 2, 3, 4]))
d

`np.random`: random numbers (Mersenne Twister PRNG)¶

a = np.random.rand(4)       # uniform in [0, 1]
a

b = np.random.randn(4)      # Gaussian
b

np.random.seed(1234)        # Setting the random seed

Basic data types¶

You may have noticed that, in some instances, array elements are displayed with a trailing dot (e.g. 2. vs 2). This is due to a difference in the data-type used:

a = np.array([1, 2, 3])
a.dtype

b = np.array([1., 2., 3.])
b.dtype

Different data-types allow us to store data more compactly in memory, but most of the time we simply work with floating point numbers. Note that, in the example above, NumPy auto-detects the data-type from the input.

You can explicitly specify which data-type you want:

c = np.array([1, 2, 3], dtype=float)
c.dtype

The default data type is floating point:

a = np.ones((3, 3))
a.dtype

There are also other types:

# Complex
d = np.array([1+2j, 3+4j, 5+6*1j])
d.dtype

# Bool
e = np.array([True, False, False, True])
e.dtype

# Strings
f = np.array(['Bonjour', 'Hello', 'Hallo',])
f.dtype     # <--- strings containing max. 7 letters

And much more…

int32
int64
uint32
uint64

Indexing and slicing¶

The items of an array can be accessed and assigned to the same way as other Python sequences (e.g. lists):

a = np.arange(10)
a

a[0], a[2], a[-1]

Warning: Indices begin at 0, like other Python sequences (and C/C++). In contrast, in Fortran or Matlab, indices begin at 1.

The usual python idiom for reversing a sequence is supported:

a[::-1]

For multidimensional arrays, indexes are tuples of integers:

a = np.diag(np.arange(3))
a

a[1, 1]

a[2, 1] = 10 # third line, second column
a

a[1]

Note¶

In 2D, the first dimension corresponds to rows, the second to columns.
For multidimensional a, a[0] is interpreted by taking all elements in the unspecified dimensions.

Slicing: Arrays, like other Python sequences can also be sliced¶

a = np.arange(10)
a

a[2:9:3] # [start:end:step]

Note that the last index is not included!

a[:4]

All three slice components are not required: by default, start is 0, end is the last and step is 1:

a[1:3]

a[::2]

a[3:]

A small illustrated summary of NumPy indexing and slicing…

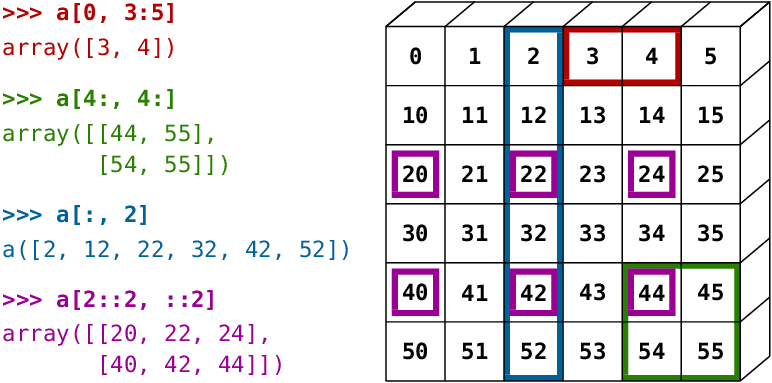
You can also combine assignment and slicing:

a = np.arange(10)
a[5:] = 10
a

b = np.arange(5)
a[5:] = b[::-1]
a

Fancy indexing¶

NumPy arrays can be indexed with slices, but also with boolean or integer arrays (masks). This method is called fancy indexing. It creates copies not views.

Using boolean masks¶

np.random.seed(3)
a = np.random.randint(0, 21, 15)
a

(a % 3 == 0)

mask = (a % 3 == 0)
extract_from_a = a[mask] # or,  a[a%3==0]
extract_from_a           # extract a sub-array with the mask

Indexing with a mask can be very useful to assign a new value to a sub-array:

a[a % 3 == 0] = -1
a

Indexing with an array of integers¶

a = np.arange(0, 100, 10)
a

Indexing can be done with an array of integers, where the same index is repeated several time:

a[[2, 3, 2, 4, 2]]  # note: [2, 3, 2, 4, 2] is a Python list

New values can be assigned with this kind of indexing:

a[[9, 7]] = -100
a

The image below illustrates various fancy indexing applications:

Elementwise operations¶

NumPy provides many elementwise operations that are much quicker than comparable list comprehension in plain Python.

Basic operations¶

With scalars:

a = np.array([1, 2, 3, 4])
a + 1

2**a

All arithmetic operates elementwise:

b = np.ones(4) + 1
a - b

a * b

j = np.arange(5)
2**(j + 1) - j

Array multiplication is not matrix multiplication¶

c = np.ones((3, 3))
c * c                   # NOT matrix multiplication!

# Matrix multiplication
c.dot(c)

Other operations¶

Comparisons¶

a = np.array([1, 2, 3, 4])
b = np.array([4, 2, 2, 4])
a == b

a > b

Array-wise comparisons:

a = np.array([1, 2, 3, 4])
b = np.array([4, 2, 2, 4])
c = np.array([1, 2, 3, 4])
np.array_equal(a, b)

np.array_equal(a, c)

Logical operations¶

a = np.array([1, 1, 0, 0], dtype=bool)
b = np.array([1, 0, 1, 0], dtype=bool)
np.logical_or(a, b)

np.logical_and(a, b)

Transcendental functions¶

a = np.arange(5)
np.sin(a)

np.log(a)

np.exp(a)

Shape mismatches¶

a = np.arange(4)

# NBVAL_SKIP
a + np.array([1, 2])

Broadcasting? We’ll return to that later.

Transposition¶

a = np.triu(np.ones((3, 3)), 1)
a

a.T

The transposition is a view¶

As a result, the following code is wrong and will not make a matrix symmetric:

>>> a += a.T

It will work for small arrays (because of buffering) but fail for large one, in unpredictable ways.

Basic reductions¶

NumPy offers many quick functions to compute things like sum, mean, max etc.

Computing sums¶

x = np.array([1, 2, 3, 4])
np.sum(x)

Note: Certain NumPy functions can be also written at the end of an Numpy array.

x.sum()

Sum by rows and by columns:

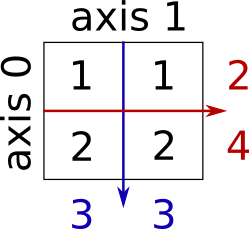
x = np.array([[1, 1], [2, 2]])
x

x.sum(axis=0)   # columns (first dimension)

x.sum(axis=1)   # rows (second dimension)

Other reductions¶

Like, mean, std, cumsum etc. works the same way (and take axis=).

Extrema¶

x = np.array([1, 3, 2])
x.min()

x.max()

x.argmin()  # index of minimum

x.argmax()  # index of maximum

Logical operations¶

np.all([True, True, False])

np.any([True, True, False])

Can be used for array comparisons:

a = np.zeros((100, 100))
np.any(a != 0)

np.all(a == a)

a = np.array([1, 2, 3, 2])
b = np.array([2, 2, 3, 2])
c = np.array([6, 4, 4, 5])
((a <= b) & (b <= c)).all()

Statistics¶

x = np.array([1, 2, 3, 1])
y = np.array([[1, 2, 3], [5, 6, 1]])
x.mean()

np.median(x)

np.median(y, axis=-1) # last axis

x.std()          # full population standard dev.

… and many more (best to learn as you go).

Broadcasting¶

Basic operations on numpy arrays (addition, etc.) are elementwise
This works on arrays of the same size. Nevertheless, It’s also possible to do operations on arrays of different sizes if NumPy can transform these arrays so that they all have the same size: this conversion is called broadcasting.

The image below gives an example of broadcasting:

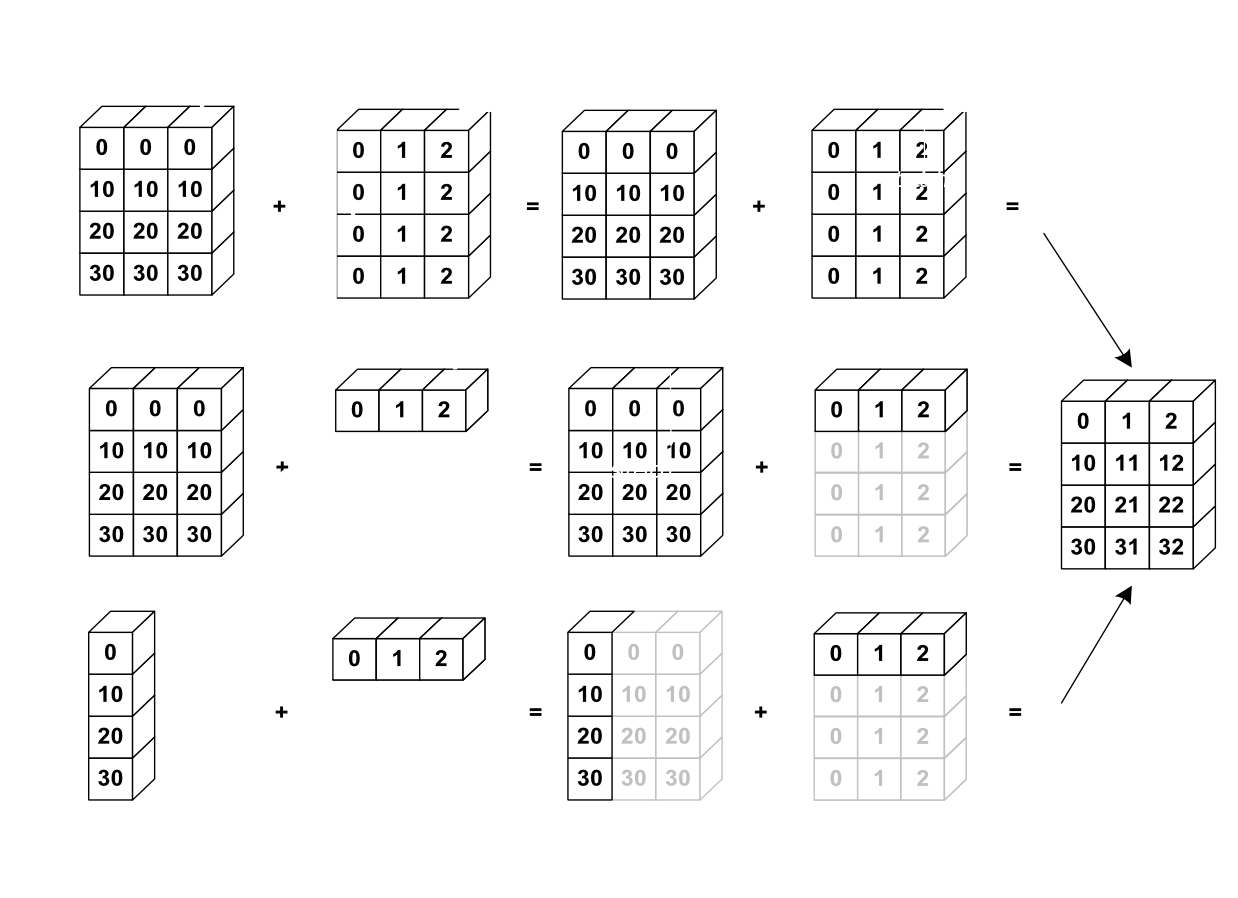
Let’s verify this:

a = np.tile(np.arange(0, 40, 10), (3, 1)).T
a

b = np.array([0, 1, 2])
a + b

We have already used broadcasting without knowing it!

a = np.ones((4, 5))
a[0] = 2  # we assign an array of dimension 0 to an array of dimension 1
a

An useful trick:

a = np.arange(0, 40, 10)
a.shape

a = a[:, np.newaxis]  # adds a new axis -> 2D array
a.shape
a

a + b

Broadcasting seems a bit magical, but it is actually quite natural to use it when we want to solve a problem whose output data is an array with more dimensions than input data.

A lot of grid-based or network-based problems can also use broadcasting. For instance, if we want to compute the distance from the origin of points on a 10x10 grid, we can do:

x, y = np.arange(5), np.arange(5)[:, None]
distance = np.sqrt(x ** 2 + y ** 2)
distance

Or in color:

Array shape manipulation¶

Sometimes your arrays don’t have the right shape. Also for this, NumPy has many solutions.

Flattening¶

a = np.array([[1, 2, 3], [4, 5, 6]])
a

a.ravel()

a.T

a.T.ravel()

Higher dimensions: last dimensions ravel out “first”.

Reshaping¶

The inverse operation to flattening:

a = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
a

a.reshape(6, 2)

Or,

a.reshape((6, -1))    # unspecified (-1) value is inferred

Adding a dimension¶

Indexing with the np.newaxis or None object allows us to add an axis to an array (you have seen this already above in the broadcasting section):

z = np.array([1, 2, 3])
z

z[:, np.newaxis]

z[np.newaxis, :]

Dimension shuffling¶

a = np.arange(4*3*2).reshape(4, 3, 2)
a

a.shape

b = a.transpose(1, 2, 0)
b

b.shape

Resizing¶

Size of an array can be changed with ndarray.resize:

a = np.arange(4)
a.resize((8,))
a

Sorting data¶

Sorting along an axis:

a = np.array([[4, 3, 5], [1, 2, 1]])
b = np.sort(a, axis=1)
b

Important: Note that the code above sorts each row separately!

In-place sort:

a.sort(axis=1)
a

Sorting with fancy indexing:

a = np.array([4, 3, 1, 2])
j = np.argsort(a)
j

a[j]

Finding minima and maxima:

a = np.array([4, 3, 1, 2])
j_max = np.argmax(a)
j_min = np.argmin(a)
j_max, j_min

`npy` - NumPy’s own data format¶

NumPy has its own binary format, not portable but with efficient I/O:

data = np.ones((3, 3))
np.save('pop.npy', data)
data3 = np.load('pop.npy')

Summary - What do you need to know to get started?¶

Know how to create arrays : array, arange, ones, zeros.
Know the shape of the array with array.shape, then use slicing to obtain different views of the array: array[::2], etc. Adjust the shape of the array using reshape or flatten it with ravel.
Obtain a subset of the elements of an array and/or modify their values with masks
a[a < 0] = 0
Know miscellaneous operations on arrays, such as finding the mean or max (array.max(), array.mean()).
For advanced use: master the indexing with arrays of integers, as well as broadcasting.

Introduction to Python

Introduction to SciPy

ML/DL with a focus on Neuroscience - SynAGE workshop

Introduction to NumPy¶

NumPy¶

Everything revolves around numpy arrays¶

NumPy arrays vs Python arrays¶

Creating arrays¶

Manual construction of arrays¶

1-D¶

2-D, 3-D, …¶

Functions for creating arrays¶

Evenly spaced¶

… or by number of points¶

Common arrays¶

np.random: random numbers (Mersenne Twister PRNG)¶

Basic data types¶

Indexing and slicing¶

Note¶

Slicing: Arrays, like other Python sequences can also be sliced¶

Fancy indexing¶

Using boolean masks¶

Indexing with an array of integers¶

Elementwise operations¶

Basic operations¶

Array multiplication is not matrix multiplication¶

Other operations¶

Comparisons¶

Logical operations¶

Transcendental functions¶

Shape mismatches¶

Transposition¶

The transposition is a view¶

Basic reductions¶

Computing sums¶

Other reductions¶

Extrema¶

Logical operations¶

Statistics¶

Broadcasting¶

Array shape manipulation¶

Flattening¶

Reshaping¶

Adding a dimension¶

Dimension shuffling¶

Resizing¶

Sorting data¶

npy - NumPy’s own data format¶

Summary - What do you need to know to get started?¶

`np.random`: random numbers (Mersenne Twister PRNG)¶

`npy` - NumPy’s own data format¶