Models, AI and all other buzz words
Contents
Models, AI and all other buzz words¶
What do these faces have in common?
https://static01.nyt.com/images/2020/11/19/us/artificial-intelligence-fake-people-faces-promo-1605818328743/artificial-intelligence-fake-people-faces-promo-1605818328743-superJumbo-v2.jpg
What is AI?
https://external-preview.redd.it/hWh_8TpqrT6zAwpzHJ_m9Rx3iHjc_yI4zSI6aazMFTc.jpg?auto=webp&s=6d8006ac3edca5bad98dd7b5b9a4a8d5554eaff0
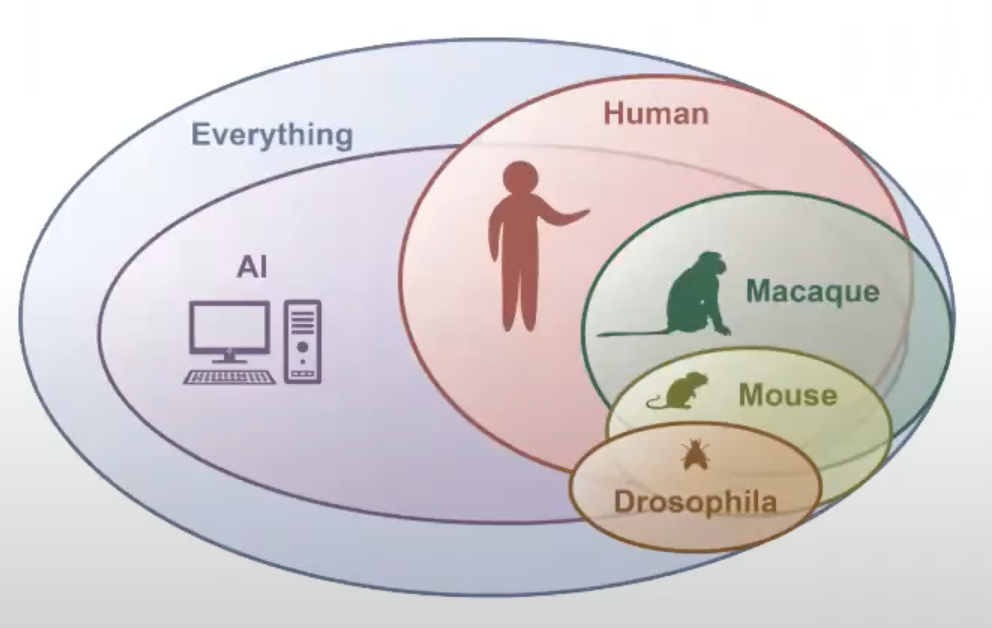
Quite often the discussion about AI centers around general artificial intelligence which might be a bit of an ill-posed problem as we don’t have any reason that “true” general artificial intelligence can exist. The focus here is on "general".
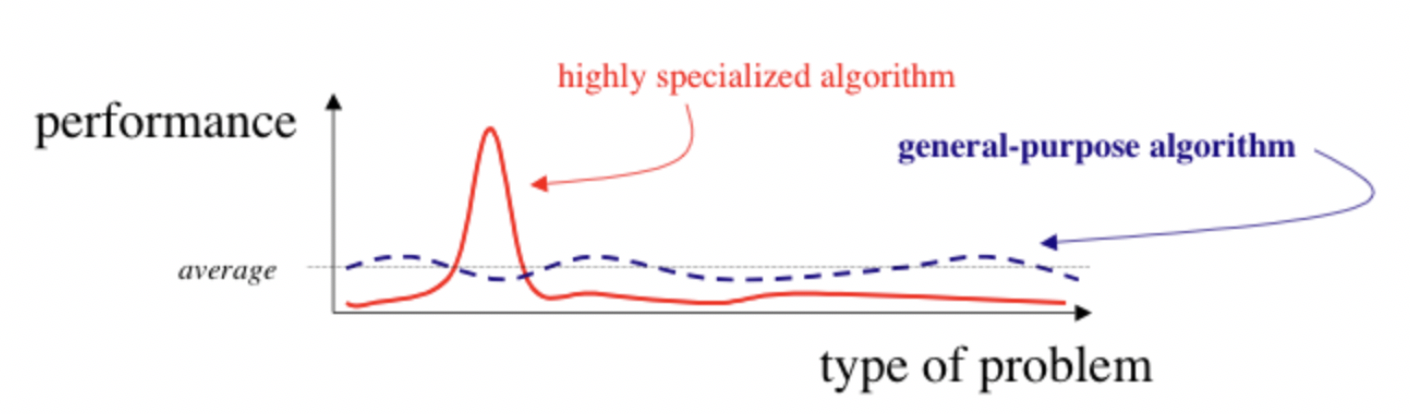
However, one thing we know that appears to be fairly general purpose is a biological brain . On the other hand it really is not as it might be applicable to many domains, but is heavily focused on a few tasks within the world it is surrounded by. This is also the idea what we should do with AI and referred to as the AI set.
The AI set
idea & definition |
graphical representation |
|---|---|
This refers to a set of |
|
And this is exactly what we’re going to talk about.
Aim(s) of this section¶
get to know the “lingo” and basic vocabulary
define important terms
situate core workflow aspects
Outline for this section¶
The definitions
The fellowship of core aspects
The two (or more) parts of each aspect
The return of the complexity
Yes, it’s that “easy”
The definitions¶
As with many other things it’s important to define central terms and aspects. Here we’re going to do that for artificial intelligence, machine learning and deep learning.
Artificial intelligence (AI) is intelligence demonstrated by machines, as opposed to the natural intelligence displayed by humans or animals. Leading AI textbooks define the field as the study of “intelligent agents”: any system that perceives its environment and takes actions that maximize its chance of achieving its goals. Some popular accounts use the term “artificial intelligence” to describe machines that mimic “cognitive” functions that humans associate with the human mind, such as “learning” and “problem solving”, however this definition is rejected by major AI researchers.
https://en.wikipedia.org/wiki/Artificial_intelligence
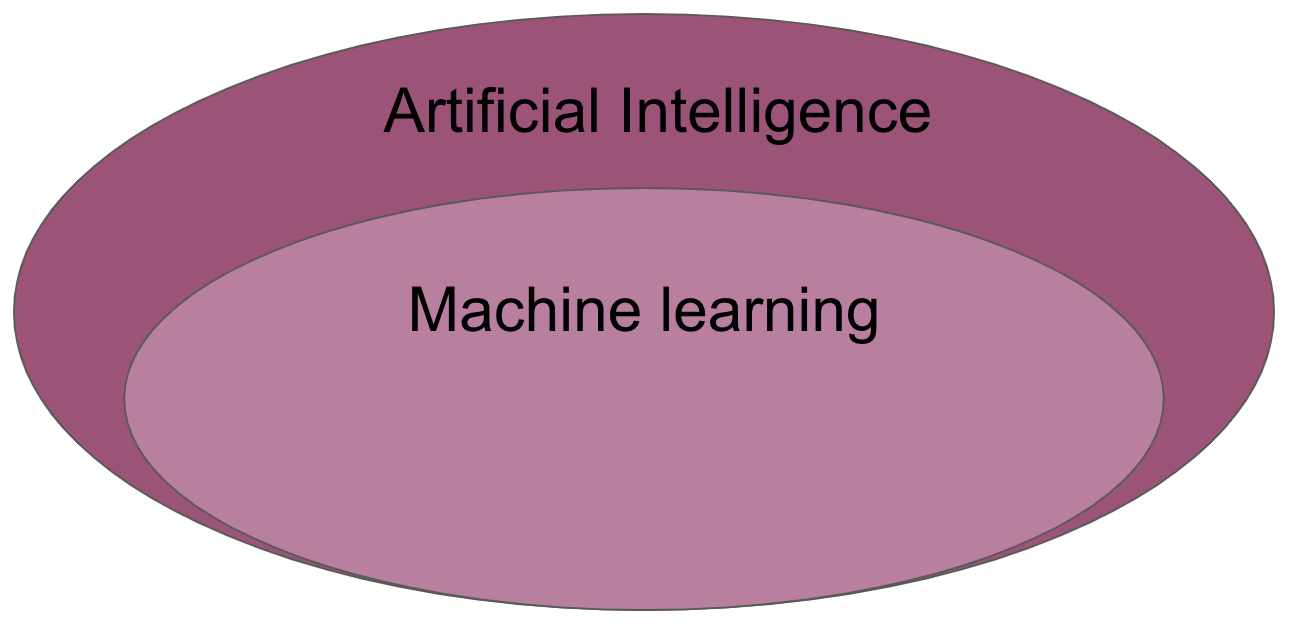
Machine learning (ML) is the study of computer algorithms that can improve automatically through experience and by the use of data. It is seen as a part of artificial intelligence. Machine learning algorithms build a model based on sample data, known as “training data”, in order to make predictions or decisions without being explicitly programmed to do so. A subset of machine learning is closely related to computational statistics, which focuses on making predictions using computers; but not all machine learning is statistical learning. The study of mathematical optimization delivers methods, theory and application domains to the field of machine learning. Data mining is a related field of study, focusing on exploratory data analysis through unsupervised learning. Some implementations of machine learning use data and neural networks in a way that mimics the working of a biological brain.
https://en.wikipedia.org/wiki/Machine_learning
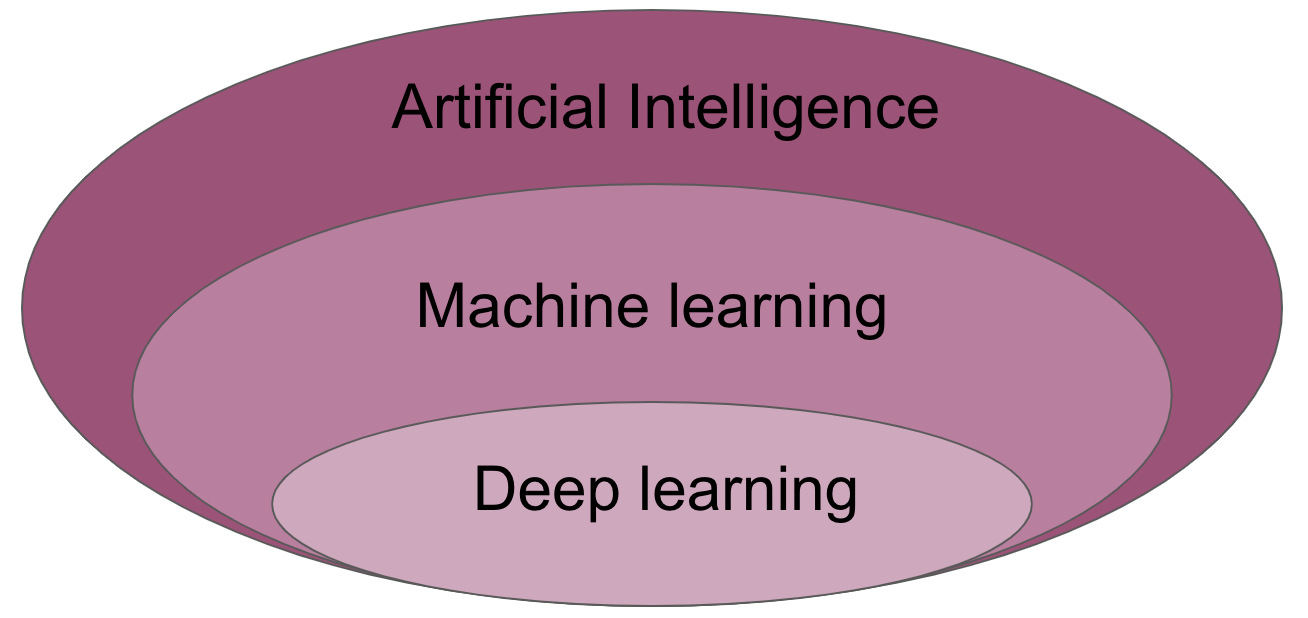
Deep learning (also known as deep structured learning) is part of a broader family of machine learning methods based on artificial neural networks with representation learning. Learning can be supervised, semi-supervised or unsupervised. Artificial neural networks (ANNs) were inspired by information processing and distributed communication nodes in biological systems. ANNs have various differences from biological brains. Specifically, neural networks tend to be static and symbolic, while the biological brain of most living organisms is dynamic (plastic) and analogue. The adjective “deep” in deep learning refers to the use of multiple layers in the network. Early work showed that a linear perceptron cannot be a universal classifier, but that a network with a nonpolynomial activation function with one hidden layer of unbounded width can.
The fellowship of core aspects¶
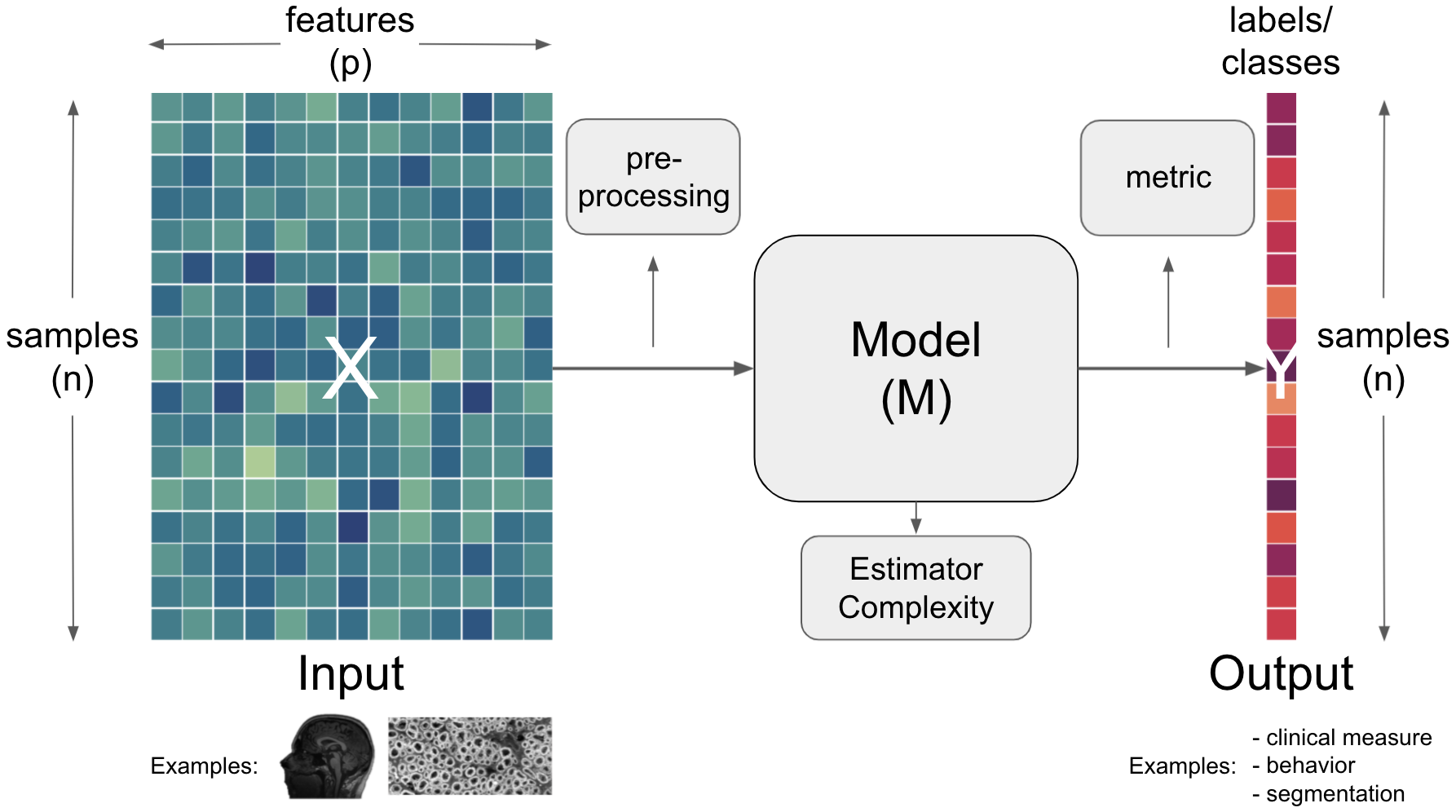
After outlining the major terms, we also need to define further concepts and vocabulary that is commonly used. We will do that based on a simplified graphical description which we will use throughout most of this part of the course. So, let’s start with what a model refers to.
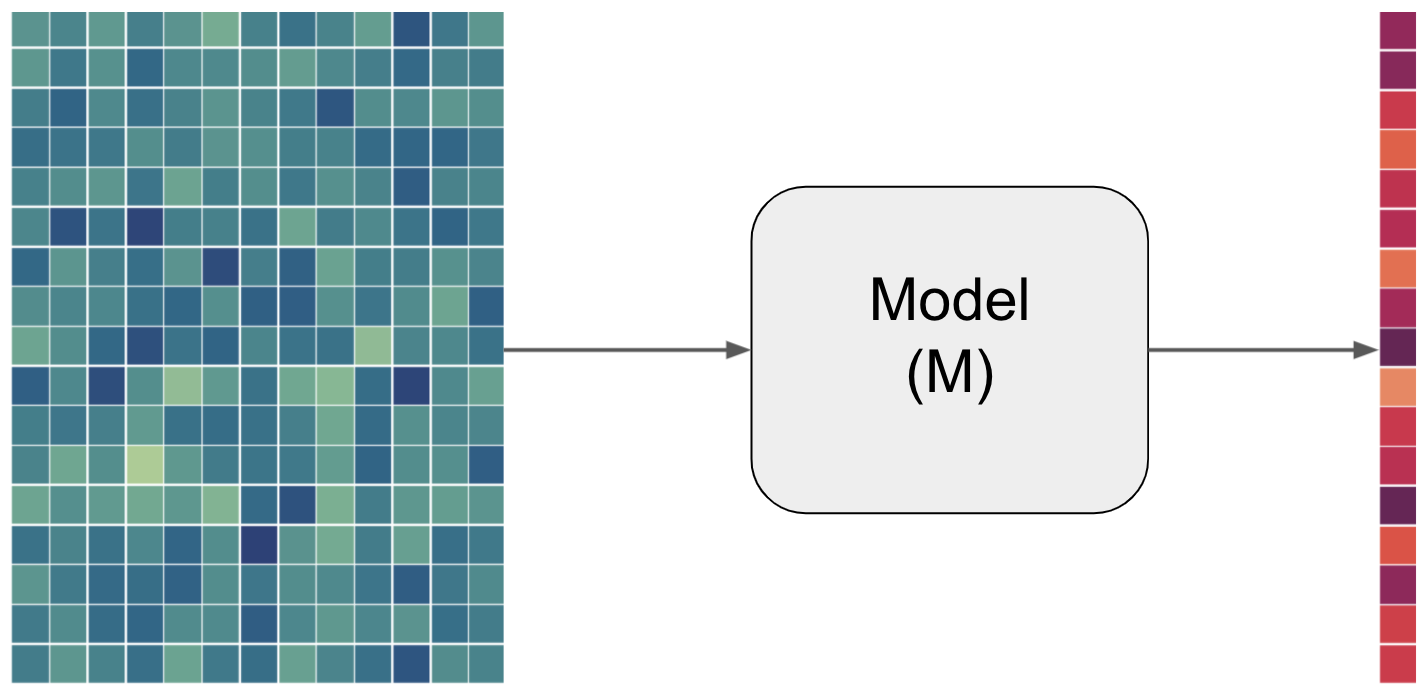
Term |
Definition |
|---|---|
Model |
A set of parameters that makes a prediction based on a given input. The parameter values are fitted to available data. |
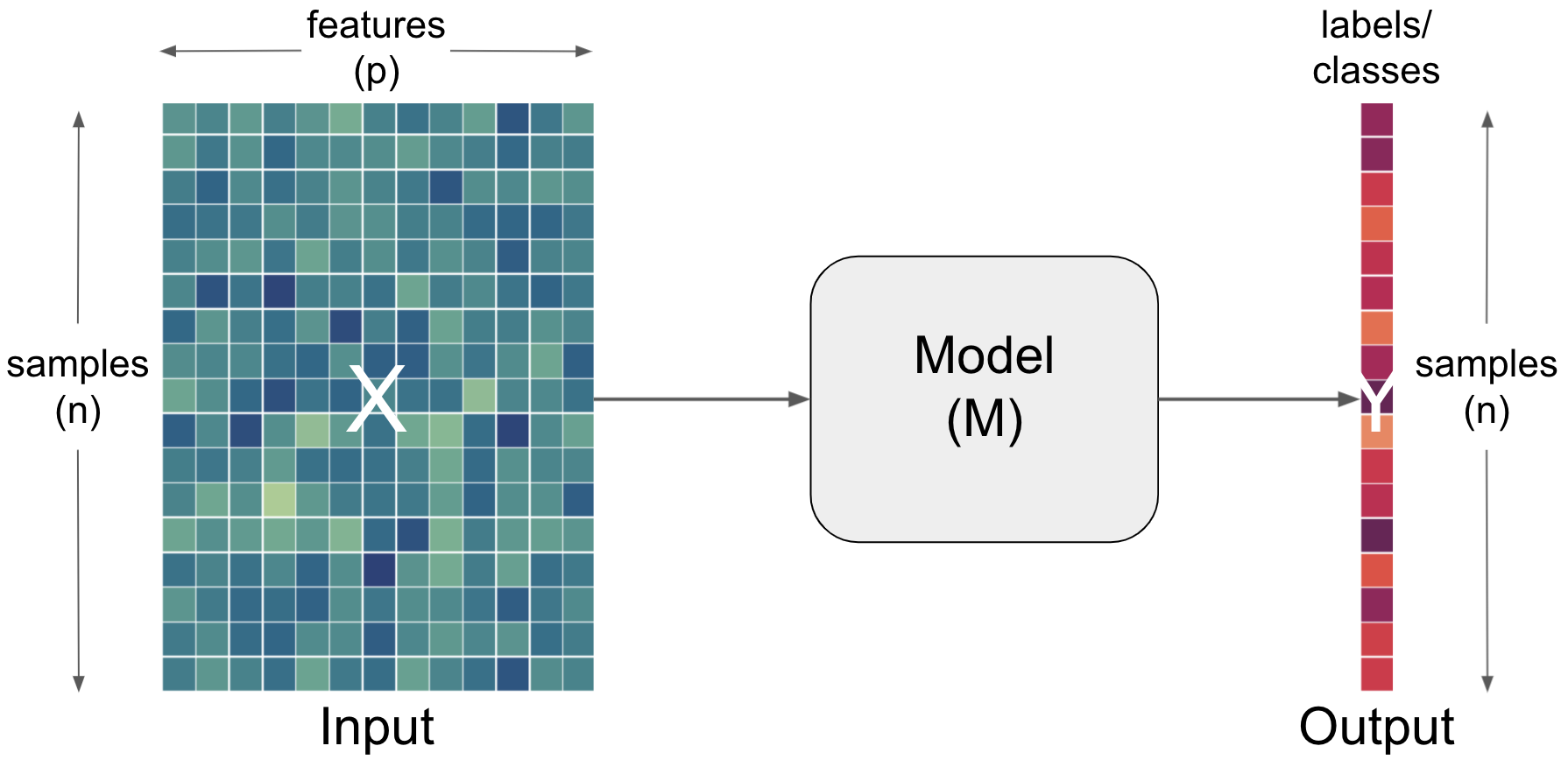
But what does input, prediction and data mean here? The input entails the data and the prediction in this case entails the output. Let’s add the respective information to our graphical description.
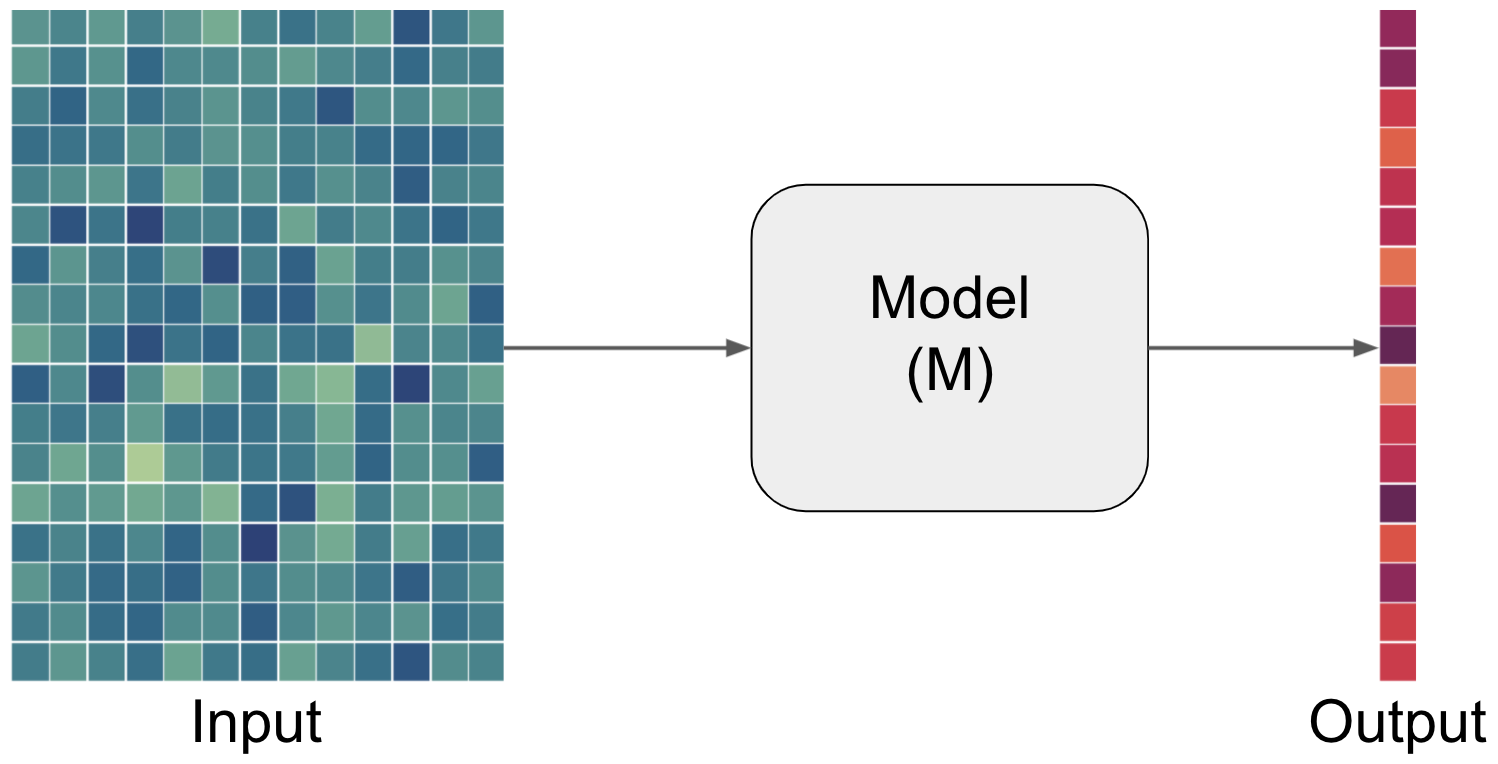
In the world of artificial intelligence (in theoretic but also practical content) you will commonly see X being used to denote the input and y denoting the output.
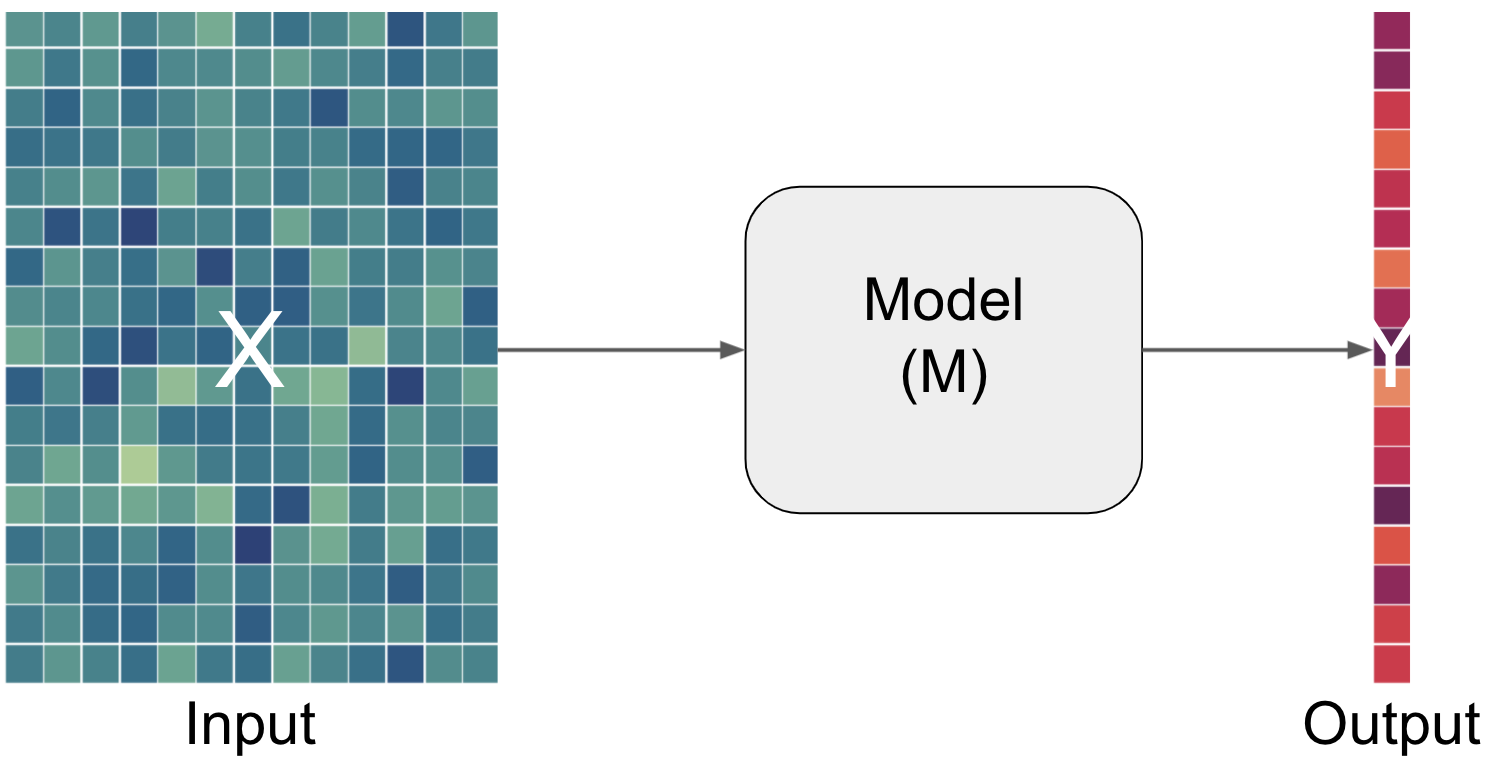
The two (or more) parts of each aspect¶
Importantly, each aspect can and has to be described and defined even further. For example, the input is usually outlined as a function of samples and features.
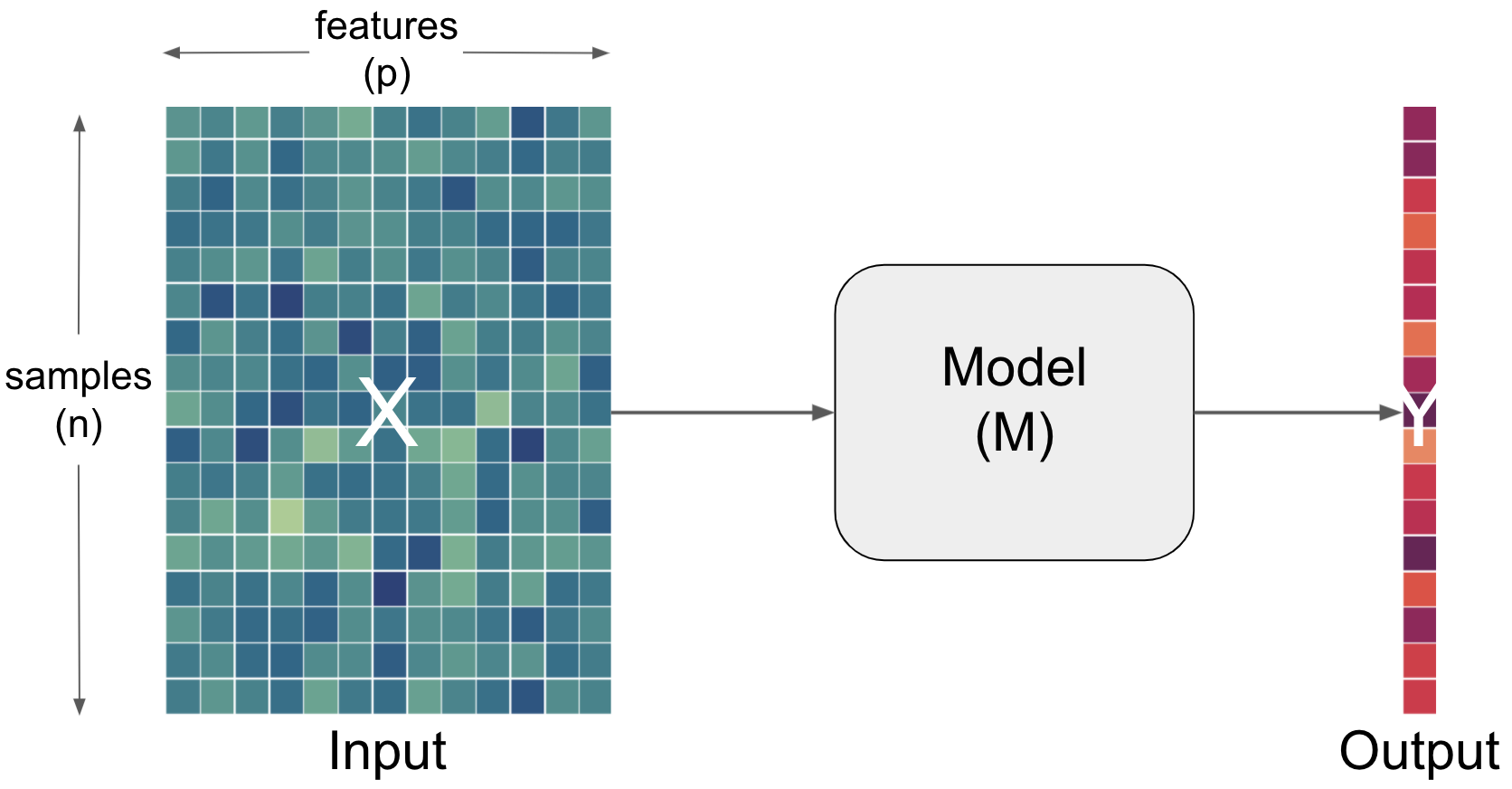
Term |
Definition |
|---|---|
Input |
Data from which we would like to make predictions. For example, results from lab tests (e.g. hematocrit, protein concentrations, response time) to inform a diagnosis (e.g. anemia, Alzheimer’s, Muliple Sclerosis). Data is typically multidimensional, with each sample having multiple values that we think might inform our predictions. Conventionally, the dimensions of data are [number of subjects] x [number of features] |
Sample |
One dimension of the |
Feature |
One dimension of the |
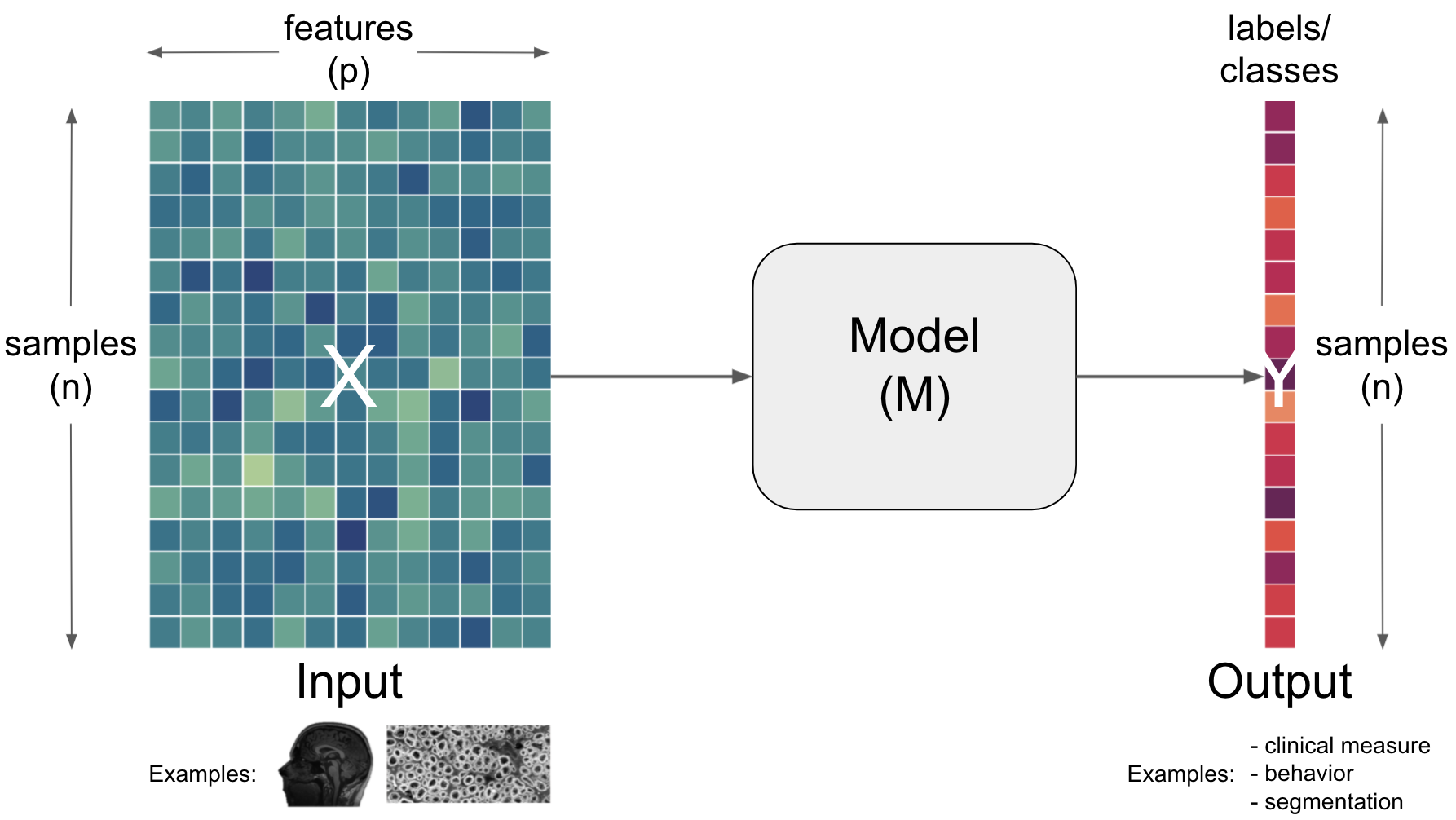
Obviously, the output can and needs to be further described/defined as well. Here, we could for example do that based on a function of samples and labels.
Term |
Definition |
|---|---|
Labels |
True values corresponding to an |
Prediction |
The |
Let’s put all of this more into the perspective of neuroscience.
The return of the complexity¶
Having outlined the core components of artificial intelligence workflows, input, model and output, we also need to talk about the many other things that are crucial. This comprises aspects situated within the core components but also “between” them. Regarding the latter, an operation commonly utilized is preprocessing.
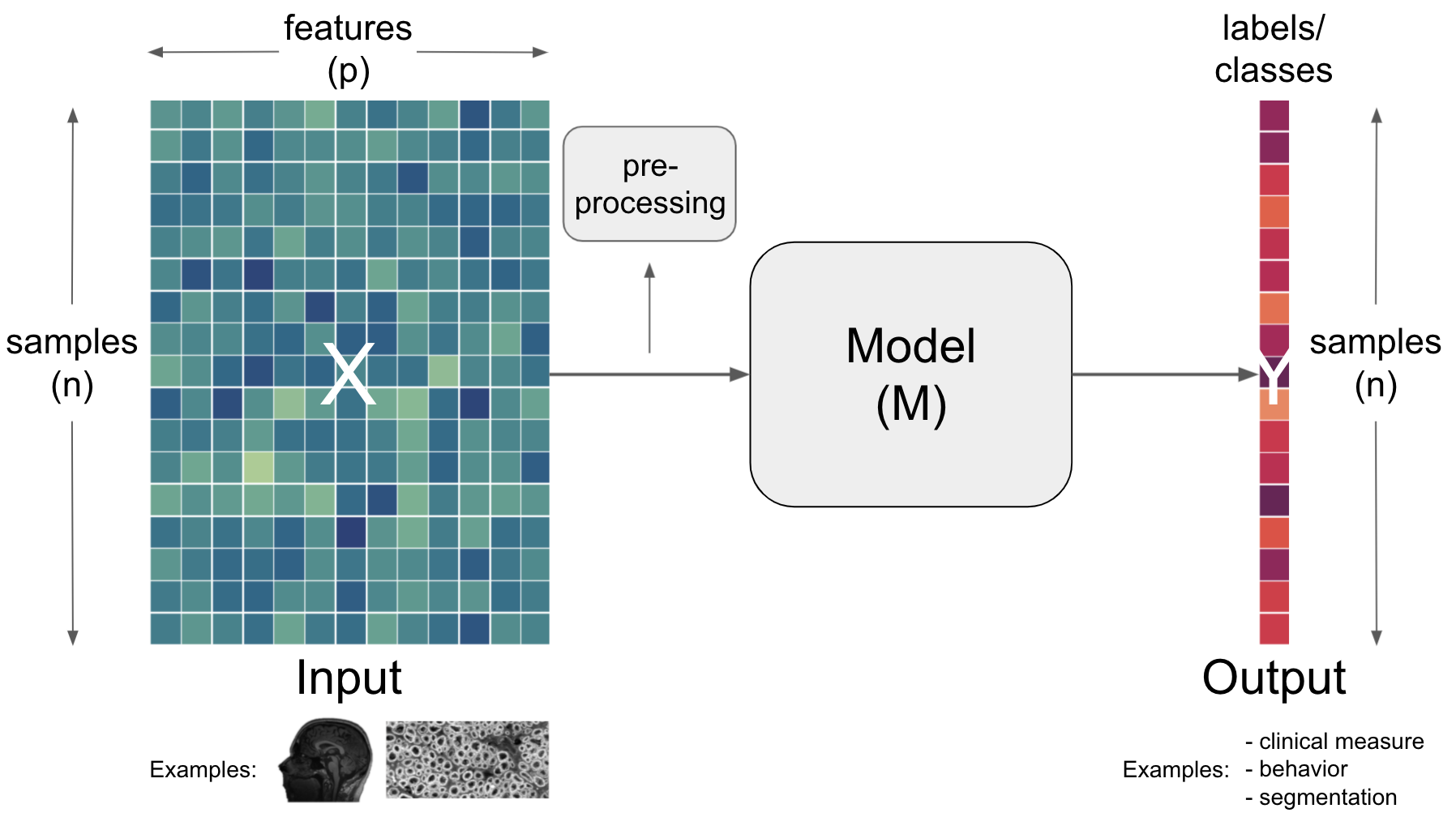
Term |
Definition |
|---|---|
Preprocessing |
Change the |
Going further concerning models, important aspects one needs to consider there are the estimator and the complexity.
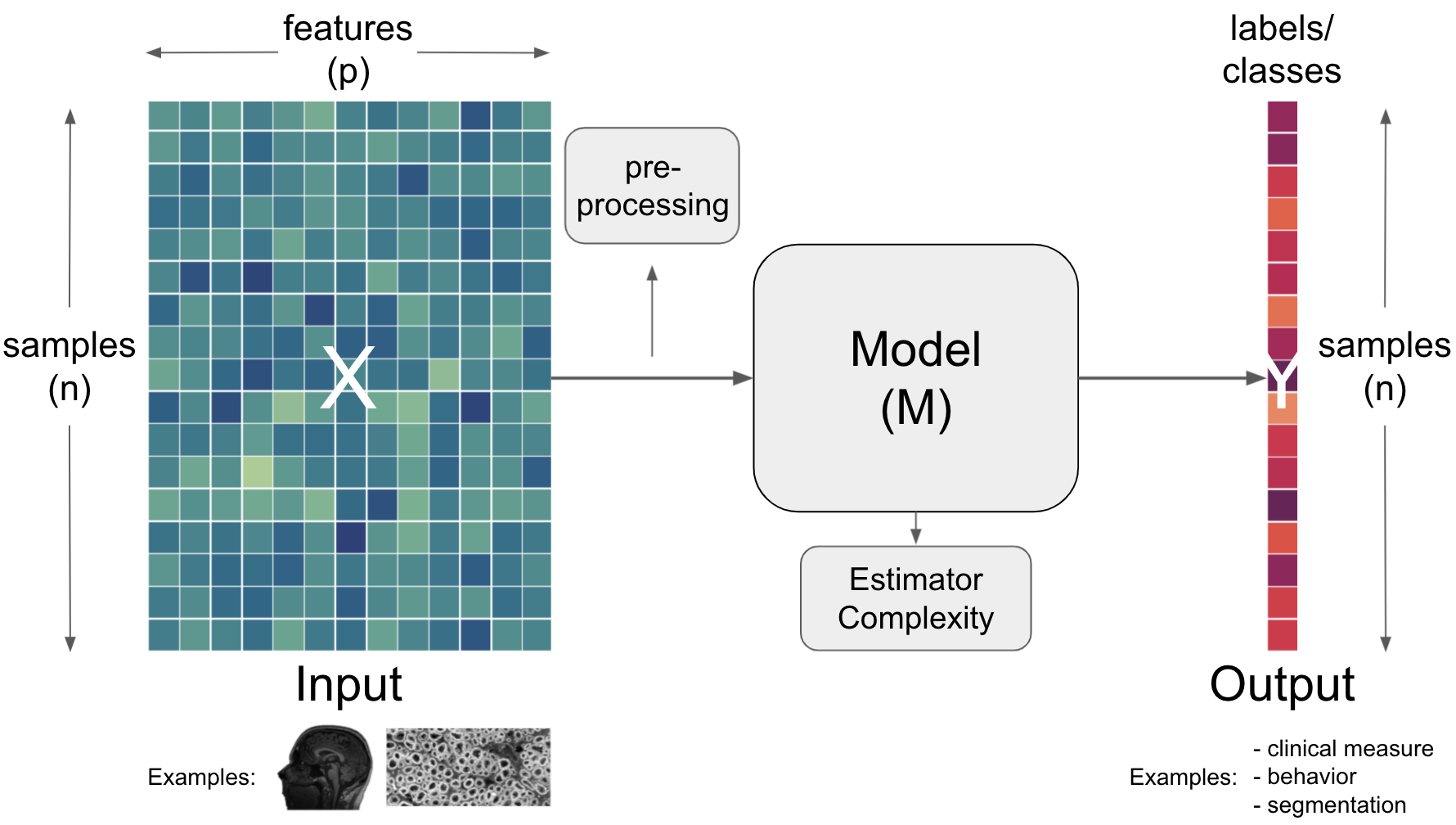
Term |
Definition |
|---|---|
Estimator |
An instance of a |
Complexity |
Refers to the number of |
Finally (at least within our short and simplified endeavour here), we need to talk about the metric that can be situated between the model and the output.
Term |
Definition |
|---|---|
Metric |
A |
Sounds like a lot, eh? Let’s see how these things look like in action…
Yes, it’s that “easy”¶
Let’s imagine we want to use the functional connectivity between brain regions to predict the age of human participants. Using python and a few of its fantastic packages, here pandas and sklearn, we can make this analysis happen in no time.
At first we get our data:
import urllib.request
url = 'https://www.dropbox.com/s/v48f8pjfw4u2bxi/MAIN_BASC064_subsamp_features.npz?dl=1'
urllib.request.urlretrieve(url, 'MAIN2019_BASC064_subsamp_features.npz')
('MAIN2019_BASC064_subsamp_features.npz',
<http.client.HTTPMessage at 0x7fca752cd7c0>)
Next, we load our input and inspect it:
import numpy as np
data = np.load('MAIN2019_BASC064_subsamp_features.npz')['a']
data.shape
(155, 2016)
We can also use plotly to easily visualize our input data in an interactive manner (please click on the + to see the code):
import plotly.express as px
from IPython.core.display import display, HTML
from plotly.offline import init_notebook_mode, plot
fig = px.imshow(data, labels=dict(x="features", y="participants"), height=800, aspect='None')
fig.update(layout_coloraxis_showscale=False)
init_notebook_mode(connected=True)
#fig.show()
plot(fig, filename = '../../../static/input_data.html')
display(HTML('../../../static/input_data.html'))
To get a better idea of what this means, let’s have a look at the feature from the neuroscience perspective, ie. the brain network (please click on the + to see the code):
from nilearn import datasets
data = datasets.fetch_development_fmri(n_subjects=1)
parcellations = datasets.fetch_atlas_basc_multiscale_2015(version='sym')
atlas_filename = parcellations.scale064
from nilearn.input_data import NiftiLabelsMasker
masker = NiftiLabelsMasker(labels_img=atlas_filename, standardize=True,
memory='nilearn_cache', verbose=1)
time_series = masker.fit_transform(data['func'][0])
from nilearn.connectome import ConnectivityMeasure
correlation_measure = ConnectivityMeasure(kind='correlation')
correlation_matrix = np.squeeze(correlation_measure.fit_transform([time_series]))
import numpy as np
# Mask the main diagonal for visualization:
#np.fill_diagonal(correlation_matrix, 0)
# The labels we have start with the background (0), hence we skip the
# first label
from nilearn.plotting import find_parcellation_cut_coords, view_connectome
coords = find_parcellation_cut_coords(atlas_filename)
view_connectome(correlation_matrix, coords, edge_threshold='80%',
title='Features displayed from a network perspective', colorbar=False)
[NiftiLabelsMasker.fit_transform] loading data from /Users/peerherholz/nilearn_data/basc_multiscale_2015/template_cambridge_basc_multiscale_nii_sym/template_cambridge_basc_multiscale_sym_scale064.nii.gz
Resampling labels
Beside the input data we also need our labels:
url = 'https://www.dropbox.com/s/ofsqdcukyde4lke/participants.csv?dl=1'
urllib.request.urlretrieve(url, 'participants.csv')
('participants.csv', <http.client.HTTPMessage at 0x7fca78887b20>)
Which we can easily load and check via pandas:
import pandas as pd
labels = pd.read_csv('participants.csv')['AgeGroup']
labels.describe()
count 155
unique 6
top 5yo
freq 34
Name: AgeGroup, dtype: object
For a better intuition, we’re going to also visualize the labels and their distribution (please click on the + to see the code):
fig = px.histogram(labels, marginal='box', template='plotly_white')
fig.update_layout(showlegend=False, width=800, height=600)
init_notebook_mode(connected=True)
#fig.show()
plot(fig, filename = '../../../static/labels.html')
display(HTML('../../../static/labels.html'))
And we’re ready to create our machine learning analysis pipeline using sklearn within we will scale our input data, train a Support Vector Machine and test its predictive performance. We import the required functions and classes:
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.pipeline import make_pipeline
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
and setup a sklearn pipeline:
pipe = make_pipeline(StandardScaler(), SVC())
After dividing our input and labels into training and test sets:
X_train, X_test, y_train, y_test = train_test_split(data, labels, random_state=0)
we can already fit our machine learning analysis pipeline to our data:
pipe.fit(X_train, y_train)
Pipeline(steps=[('standardscaler', StandardScaler()), ('svc', SVC())])
and test its predictive performance:
print('accuracy is %s with chance level being %s'
%(accuracy_score(pipe.predict(X_test), y_test), 1/len(pd.unique(labels))))
accuracy is 0.5897435897435898 with chance level being 0.16666666666666666
but wait…there’s much more to talk about here
You lied!
I’m sorry.
The truth is: while it’s very easy (maybe too easy?) to setup and run machine learning analyses, doing it right is definitely not (like a lot of other complex analyses)… There are so many aspects to think about and so many things one can vary that the garden of forking paths becomes tremendously large. Thus, we will spent the next few hours to go through central concepts and components of these analyses, first for “classic” machine learning and then for deep learning.
One aspect that is part of every model is the fitting, i.e. the learning of model weights (machine learning much?. Thus, we need to go through some things there as well…
Model fitting¶
when talking about
model fitting, we need to talk about three central aspects:the model
the loss function
the optimization
Term |
Definition |
|---|---|
Model |
A set of parameters that makes a prediction based on a given input. The parameter values are fitted to available data. |
Loss function |
A function that evaluates how well your algorithm models your dataset |
Optimization |
A function that tries to minimize the loss via updating model parameters. |
An example: linear regression¶
Model: $\(y=\beta_{0}+\beta_{1} x_{1}^{2}+\beta_{2} x_{2}^{2}\)$
Loss function: $\( M S E=\frac{1}{n} \sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}\)$
optimization: Gradient descent
Gradient descentwith asingle input variableandn samplesStart with random weights (
β0andβ1) $\(\hat{y}_{i}=\beta_{0}+\beta_{1} X_{i}\)$Compute loss (i.e.
MSE) $\(M S E=\frac{1}{n} \sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}\)$Update
weightsbased on thegradient
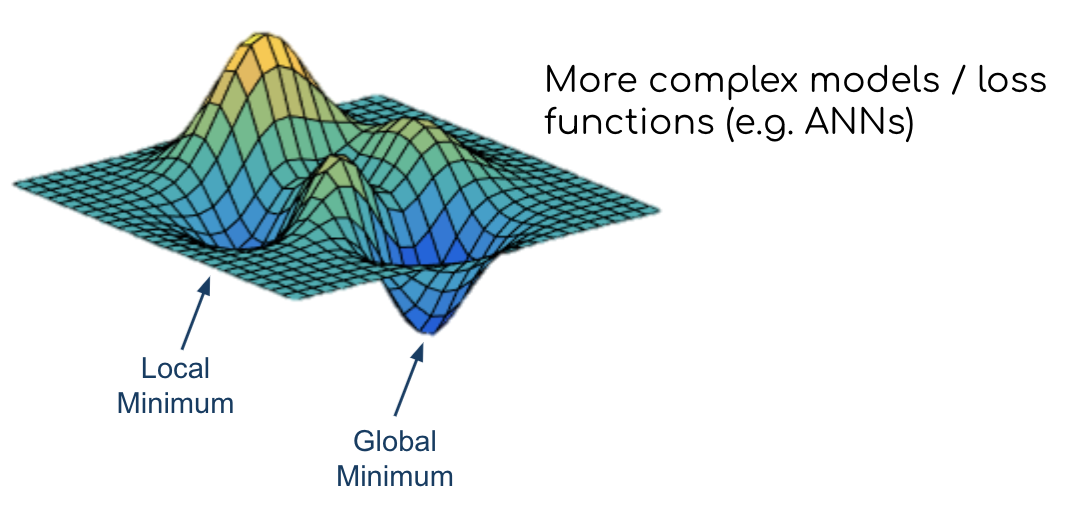
Gradient descentfor complex models withnon-convex loss functionsStart with random weights (
β0andβ1) $\(\hat{y}_{i}=\beta_{0}+\beta_{1} X_{i}\)$Compute loss (i.e.
MSE) $\(M S E=\frac{1}{n} \sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}\)$Update
weightsbased on thegradient
Questions¶
