.ipynb .pdf

repository open issue suggest edit

Binder

Contents

Functional connectivity

Objectives

In the chapter on activation maps in fMRI, we saw that this type of analysis emphasizes the notion of functional segregation, i.e. to what extent certain brain regions are involved specifically by a certain category of cognitive processes. But it is well known that cognitive processes also require some degree of functional integration, where different regions of the brain interact together to perform a task. This notion of integration leads us to conceive of the brain as a network, or even a graph, which describes the functional connectivity between regions of the brain. This chapter introduces basic concepts used to study brain connectivity using fMRI.

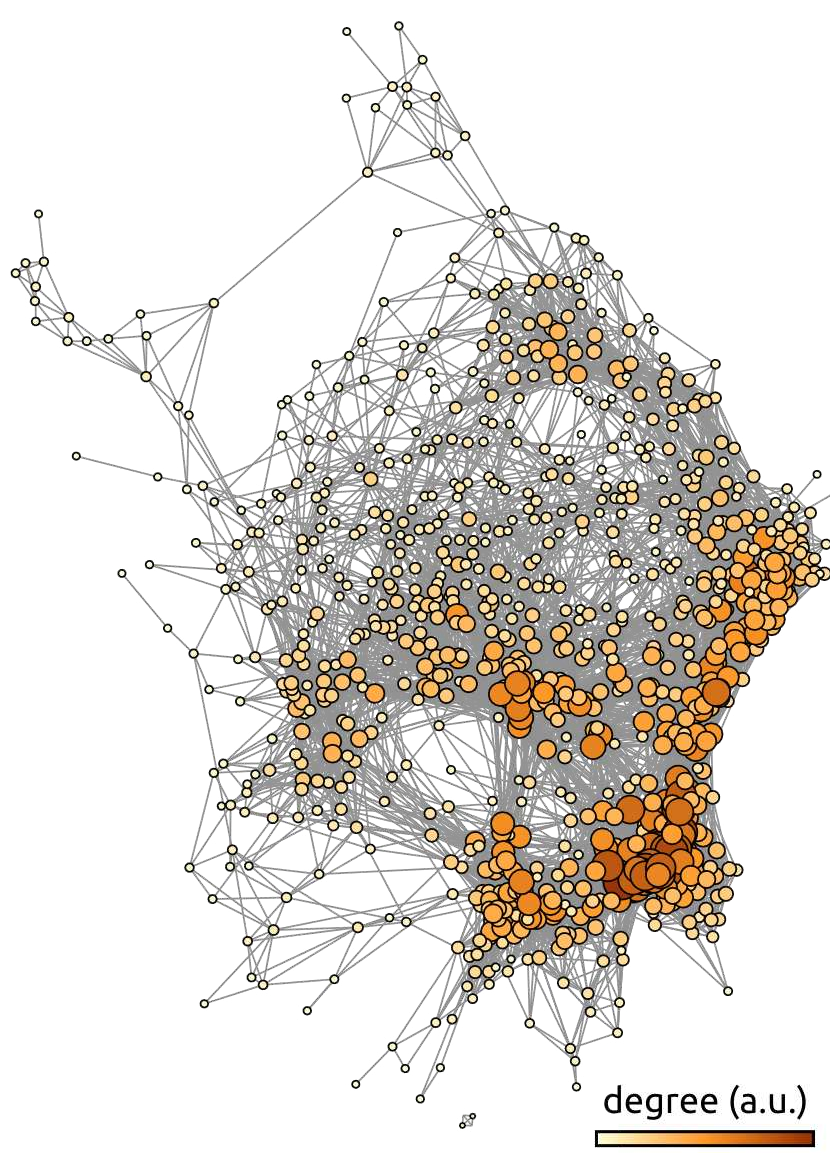
Fig. 83 Average functional connectivity graph on the ADHD-200 dataset. Each node in the graph represents a brain region, and the connections represent the average functional connectivity on the ADHD-200 [Milham et al., 2012] dataset, after thresholding. The color scale and node size represent the number of connections (degree) associated with each node. The graph is generated using the gephi library. The figure is taken from [Bellec et al., 2017], licensed under CC-BY.

The specific objectives of the chapter are to:

• Understand the definition of functional connectivity.

• Understand the distinction between intrinsic and evoked activity.

• Understand the notion of functional network.

• Know the main idle networks.

Functional connectivity cards

# Import libraries
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from nilearn.image import math_img
from nilearn import plotting, input_data
from nilearn.input_data import NiftiLabelsMasker
from nilearn import datasets # Fetch data using nilearn
from nilearn.input_data import NiftiMasker

# ignore warnings
import warnings
warnings.filterwarnings("ignore")

# Initialize the figure
fig = plt.figure(figsize=(10, 13), dpi=300)

# Import data
basc = datasets.fetch_atlas_basc_multiscale_2015() # the BASC multiscale atlas
adhd = datasets.fetch_adhd(n_subjects=10)          # ADHD200 preprocessed data (Athena pipeline)\

# Pre-processing parameters
num_data = 6
fwhm = 8
high_pass = 0.01
high_variance_confounds = False
time_samp = range(0, 100)

# Extract the signal by plot for a functional atlas (BASC)
masker = input_data.NiftiLabelsMasker(
                                      basc['scale122'],
                                      resampling_target="data",
                                      high_pass=high_pass,
                                      t_r=3,
                                      high_variance_confounds=high_variance_confounds,
                                      standardize=True,
                                      memory='nilearn_cache',
                                      memory_level=1,
                                      smoothing_fwhm=fwhm).fit()
tseries = masker.transform(adhd.func[num_data])
print(f"Time series with shape {tseries.shape} (# time points, # parcels))")

# Load data by voxel
masker_voxel = input_data.NiftiMasker(high_pass=high_pass,
                                      t_r=3,
                                      high_variance_confounds=high_variance_confounds,
                                      standardize=True,
                                      smoothing_fwhm=fwhm
                                     ).fit(adhd.func[num_data])
tseries_voxel = masker_voxel.transform(adhd.func[num_data])
print(f"Time series with shape {tseries_voxel.shape} (# time points, # voxels))")

# Show a parcel
ax_plot = plt.subplot2grid((4, 3), (0, 0), colspan=2)
num_parcel = 73
plotting.plot_roi(math_img(f'img == {num_parcel}', img=basc['scale122']),
                  threshold=0.5,
                  axes=ax_plot,
                  vmax=1,
                  title="target region (right M1)")

# plot the time series of a region
ax_plot = plt.subplot2grid((4, 3), (0, 2), colspan=1)
time = np.linspace(0, 3 * (tseries.shape[0]-1), tseries.shape[0])
plt.plot(time[time_samp], tseries[time_samp, :][:, num_parcel], 'o-'),
plt.xlabel('Time (s.)'),
plt.ylabel('BOLD (u.a.)')
plt.title('Time series')

# connectivity map
ax_plot = plt.subplot2grid((4, 3), (1, 0), colspan=2)
seed_to_voxel_correlations = (np.dot(tseries_voxel.T, tseries[:, num_parcel-1]) / tseries.shape[0])# Show the connectivity map
conn_map = masker_voxel.inverse_transform(seed_to_voxel_correlations.T)
plotting.plot_stat_map(conn_map,
                       threshold=0.5,
                       vmax=1,
                       axes=ax_plot,
                       cut_coords=(37, -20, 59),
                       title="connectivity map (right M1)")

# Show a parcel
num_parcel = 17
ax_plot = plt.subplot2grid((4, 3), (2, 0), colspan=2)
plotting.plot_roi(math_img(f'img == {num_parcel}', img=basc['scale122']),
                  threshold=0.5,
                  vmax=1,
                  axes=ax_plot,
                  title="target region (PCC)")

# plot the time series of a region
ax_plot = plt.subplot2grid((4, 3), (2, 2), colspan=1)
time = np.linspace(0, 3 * (tseries.shape[0]-1), tseries.shape[0])
plt.plot(time[time_samp], tseries[time_samp, :][:, num_parcel], 'o-'),
plt.xlabel('Time (s.)'),
plt.ylabel('BOLD (u.a.)')
plt.title('Time series')


# connectivity map
ax_plot = plt.subplot2grid((4, 3), (3, 0), colspan=2)
seed_to_voxel_correlations = (np.dot(tseries_voxel.T, tseries[:, num_parcel-1]) / tseries.shape[0])# Show the connectivity map
conn_map = masker_voxel.inverse_transform(seed_to_voxel_correlations.T)
plotting.plot_stat_map(conn_map,
                       threshold=0.5,
                       cut_coords=(0, -52, 26),
                       vmax=1,
                       axes=ax_plot,
                       title="connectivity map (PCC)")

from myst_nb import glue
glue("fcmri-map-fig", fig, display=False)

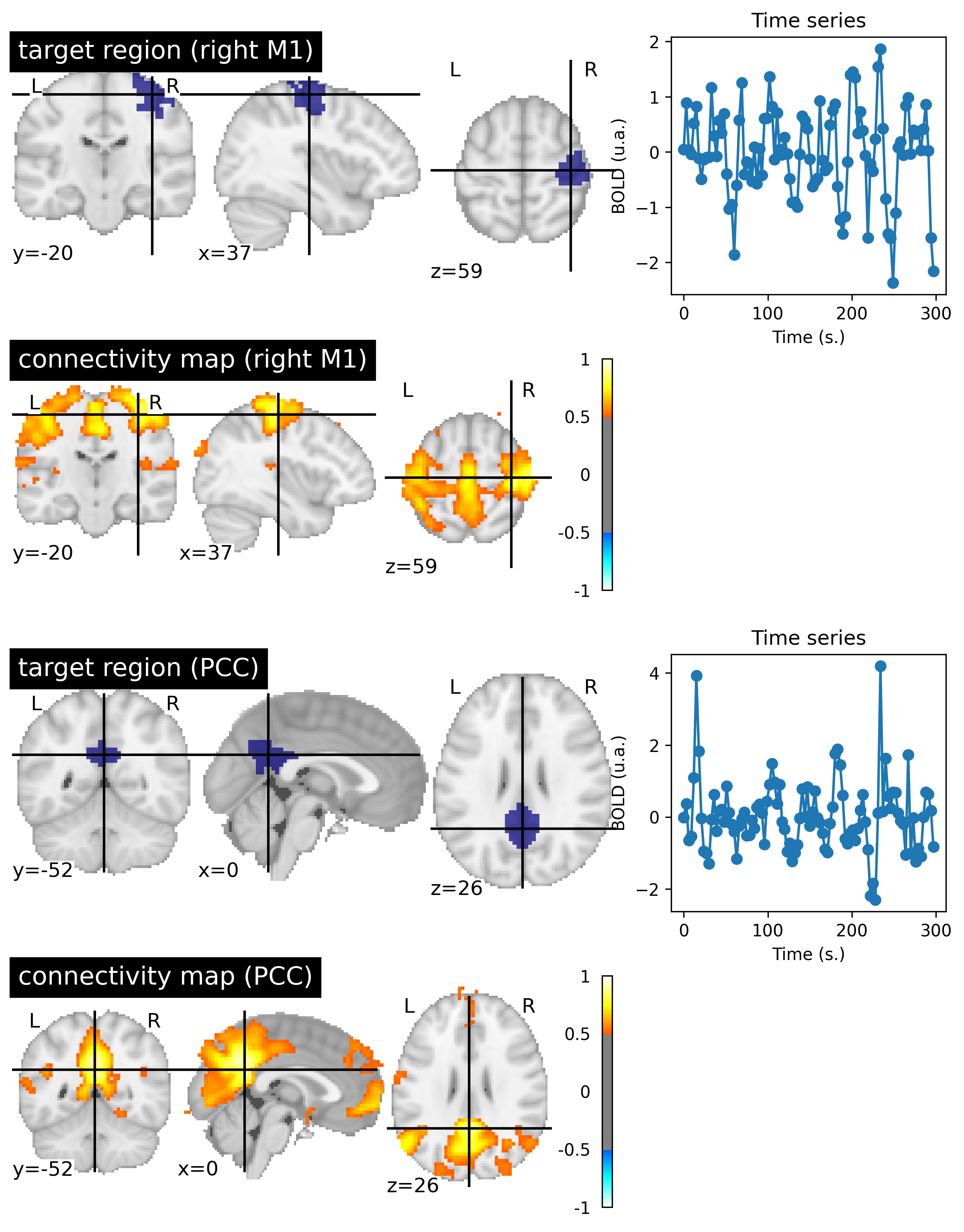
Fig. 84 Resting state connectivity maps generated from fMRI data of an individual from the ADHD-200 dataset [Milham et al., 2012]. For each map, the target region used as well as the first five minutes of BOLD activity associated with the target region are shown. This figure is generated by python code using the nilearn library (click on + to see the code), and is distributed under CC-BY license.

Before talking about functional connectivity, let’s revisit the concept of activation maps in fMRI. As we saw <activation-section>, an activation map is generated by comparing the BOLD fluctuations in a given region of the brain with a prediction of the brain response associated with a task. In a simplified way, the activation map shows us the correlation between the expected activity (based on the experimental paradigm and a hemodynamic response function) and the activity measured at each voxel.

A connectivity map is somewhat of the same logic. But instead of looking at the expected response to a task, we’re going to look at the activity of a particular region of the brain, called the target region. We will then measure the correlation between the time course of each voxel in the brain and the time course of the target region. We will obtain a functional connectivity map which shows us which regions of the brain have a highly correlated (or synchronous) activity with the target region.

Correlation measurement

The correlation between two time series is a measure that (usually) varies between -1 and 1. If the two series are identical (at their mean and variance), the correlation is 1. If the two series are statistically independent, the correlation is close to zero. If the two series mirror each other, the correlation is -1.

Functional connectivity is a relatively generic term used to describe a set of techniques for analyzing spatial patterns of brain activity [Fox and Raichle, 2007]. Fox and Raischle (2007) propose that the simplest technique to conduct this kind of analysis is indeed to extract the BOLD time course of a target region and determine its correlation with the remaining voxels. More sophisticated techniques have been developed to overcome the limitations of this modeling. They will be discussed at the end of this chapter.

The concept of a functional map was introduced by Biswal and colleagues (1995) [Biswal et al., 1995], using a target in the right primary sensorimotor cortex. This target region had been obtained with an activation map and a motor task. Biswal and colleagues then came up with the idea of observing BOLD fluctuations in a resting condition, in the absence of an experimental task. This map reveals a distributed set of regions (see Fig. 84, target M1 right), which includes the left sensorimotor cortex, but also the supplementary motor area, the premotor cortex, and other regions known for their involvement in the motor network. This study initially generated a great deal of skepticism, on the grounds that these correlated functional activity patterns could have reflected heart or breath confounds.

Slow fluctuations

Another key observation by [Biswal et al., 1995] is that the resting BOLD signal is dominated by slow fluctuations, with bursts of activity lasting 20-30 seconds , clearly visible in the Fig. 84. More specifically, the BOLD signal spectrum at rest is dominated by frequencies below 0.08 Hz, and even 0.03-0.05 Hz.

The credibility of resting connectivity maps was enhanced when different research groups were able to identify other networks using different target regions, including the visual network and the auditory network. But it was the study by Greicius and collaborators, in 2003 [Greicius et al., 2003], that sparked enormous interest in resting connectivity maps using a target region in the posterior cingulate cortex (PCC) to identify a network that had not yet been identified: the default mode network (see :refnum:`fcmri-map-fig`, PCC target). We will discuss in the next section the origins of this network, and how it can help us understand what resting state connectivity measures. It is also important to mention that the work of Shmuel and colleagues (2008) [Shmuel and Leopold, 2008] demonstrated that resting state BOLD activity correlates with spontaneous fluctuations of neural activity in the visual cortex of a anesthetized macaque, demonstrating that functional connectivity at least partially reflects the synchrony of neuronal activity, and not simply physiological noise (cardiac, respiration).

Intra- and inter-individual variability

The Fig. 84 can make connectivity networks appear extremely stable. In reality, connectivity maps vary a lot over time, ie by looking at different windows of activity for the same individual, and also between individuals. Indeed, the coordinates of a target region may be partially inaccurate even if the images are registered. Characterizing the intra- and inter-individual variability of connectivity maps is an active area of research.

The default mode network

# Import libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from nilearn import datasets
from nilearn.image import math_img
from nilearn import image
from nilearn import masking
from nilearn.glm.first_level import FirstLevelModel
from nilearn import input_data
from nilearn.input_data import NiftiLabelsMasker
from nilearn.input_data import NiftiMasker
from nilearn import plotting

# Initialize the figure
fig = plt.figure(figsize=(8, 4))

# load fMRI data
subject_data = datasets.fetch_spm_auditory()
fmri_img = image.concat_imgs(subject_data.func)

# Make an average
mean_img = image.mean_img(fmri_img)
mask = masking.compute_epi_mask(mean_img)

# Clean and smooth data
fmri_img = image.clean_img(fmri_img, high_pass=0.01, t_r=7, standardize=False)
fmri_img = image.smooth_img(fmri_img, 8.)

# load events
events = pd.read_table(subject_data['events'])

# Fit model
fmri_glm = FirstLevelModel(t_r=7,
                           drift_model='cosine',
                           signal_scaling=False,
                           mask_img=mask,                           
                           minimize_memory=False)

fmri_glm = fmri_glm.fit(fmri_img, events)

# Extract activation clusters
z_map = fmri_glm.compute_contrast('active - rest')

# plot activation map
ax_plot = plt.gca()
plotting.plot_stat_map(
        z_map, threshold=2, vmax=5, figure=fig,
        axes=ax_plot, colorbar=True, cut_coords=(3., -21, 45), bg_img=mean_img, title='activation map (auditory)')

# Glue the figure
from myst_nb import glue
glue("deactivation-fig", fig, display=False)

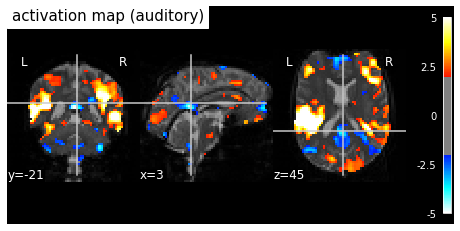
Fig. 85 Individual activation map in an auditory paradigm (spm_auditory dataset). The significance level is liberally selected (|z|>2). Moderate deactivation is identified in different regions of the brain, including the posterior cingulate cortex (PCC) and the medial prefrontal cortex (mPFC). The PCC and mPFC are key regions of the default mode network. This figure is generated by python code using the nilearn library (click on + to see the code), and is distributed under CC-BY license.

The discovery of the default mode was carried out through the study of activation, in PET. In 1997, Shulman and colleagues [Shulman et al., 1997] combined 9 PET studies that used the same "resting" control condition (consisting of passively looking at visual stimuli), and varied cognitively demanding tasks . The authors demonstrate that a set of regions are systematically more involved at rest than during the task, including in particular the posterior cingulate cortex (PCC). In 2001, Gusnard and Raichle [Raichle et al., 2001] build on the study by Shulman et al. to formulate the now famous “default mode hypothesis”. There would be a number of introspective cognitive processes that would be consistently present in a resting state, and there would be a functional network that would support this "default" activity. To confirm this hypothesis, Greicius and colleagues [Greicius et al., 2003] used an fMRI resting connectivity map with a target region in the PCC, and identified a spatially very similar resting spontaneous activity network default mode network, see :refnum:`fcmri-map-fig`. The network context of the default mode has since evolved, see the review by Buckner and DiNicola (2019) [Buckner and DiNicola, 2019] for a recent review of its neuroanatomy and cognitive roles.

# Import libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from nilearn import datasets
from nilearn.image import math_img
from nilearn import image
from nilearn import masking
from nilearn.glm.first_level import FirstLevelModel
from nilearn import input_data
from nilearn.input_data import NiftiLabelsMasker
from nilearn.input_data import NiftiMasker
from nilearn import plotting

# Initialize the figure
fig = plt.figure(figsize=(12,8))

# Import data
basc = datasets.fetch_atlas_basc_multiscale_2015() # the BASC multiscale atlas
adhd = datasets.fetch_adhd(n_subjects=10)          # ADHD200 preprocessed data (Athena pipeline)\

# Pre-processing parameters
num_data = 1
fwhm = 8
high_pass = 0.01
high_variance_confounds = False
time_samp = range(0, 100)

# Extract the signal for a functional atlas (BASC)
masker = input_data.NiftiLabelsMasker(
                                      basc['scale122'],
                                      resampling_target="data",
                                      high_pass=high_pass,
                                      t_r=3,
                                      high_variance_confounds=high_variance_confounds,
                                      standardize=True,
                                      memory='nilearn_cache',
                                      memory_level=1,
                                      smoothing_fwhm=fwhm).fit()
tseries = masker.transform(adhd.func[num_data])
print(f"Time series with shape {tseries.shape} (# time points, # parcels))")

# Load data by voxel
masker_voxel = input_data.NiftiMasker(high_pass=high_pass,
                                      t_r=3,
                                      high_variance_confounds=high_variance_confounds,
                                      standardize=True,
                                      smoothing_fwhm=fwhm
                                     ).fit(adhd.func[num_data])
tseries_voxel = masker_voxel.transform(adhd.func[num_data])
print(f"Time series with shape {tseries_voxel.shape} (# time points, # voxels))")

# Applies global signal correction
from nilearn.signal import clean as signal_clean
gb_signal = signal_clean(
                        tseries.mean(axis=1).reshape([tseries.shape[0], 1]),
                        high_pass=high_pass,
                        t_r=3,
                        standardize=True)
tseries = masker.transform(adhd.func[num_data], confounds=gb_signal)
tseries_voxel = masker_voxel.transform(adhd.func[num_data], confounds=gb_signal)

# Show a parcel
ax_plot = plt.subplot2grid((2, 3), (0, 0), colspan=2)
num_parcel = 113
plotting.plot_roi(math_img(f'img == {num_parcel}', img=basc['scale122']),
                  threshold=0.5,
                  axes=ax_plot,
                  vmax=1,
                  title="target region (FEF)")

# plot la série temporelle d'une région
ax_plot = plt.subplot2grid((2, 3), (0, 2), colspan=1)
time = np.linspace(0, 3 * (tseries.shape[0]-1), tseries.shape[0])
plt.plot(time[time_samp], tseries[time_samp, :][:, num_parcel], 'o-'),
plt.xlabel('Time (s.)'),
plt.ylabel('BOLD (u.a.)')
plt.title('Time series')

# connectivity map
ax_plot = plt.subplot2grid((2, 3), (1, 0), colspan=2)
seed_to_voxel_correlations = (np.dot(tseries_voxel.T, tseries[:, num_parcel-1]) / tseries.shape[0])# Show the connectivity map
conn_map = masker_voxel.inverse_transform(seed_to_voxel_correlations.T)
plotting.plot_stat_map(conn_map,
                       threshold=0.2,
                       vmax=1,
                       axes=ax_plot,
                       cut_coords=(-28, 2, 28),
                       display_mode = 'x',
                       title="connectivity map (FEF)")

# Glue the figure
from myst_nb import glue
glue("negative-DMN-fig", fig, display=False)

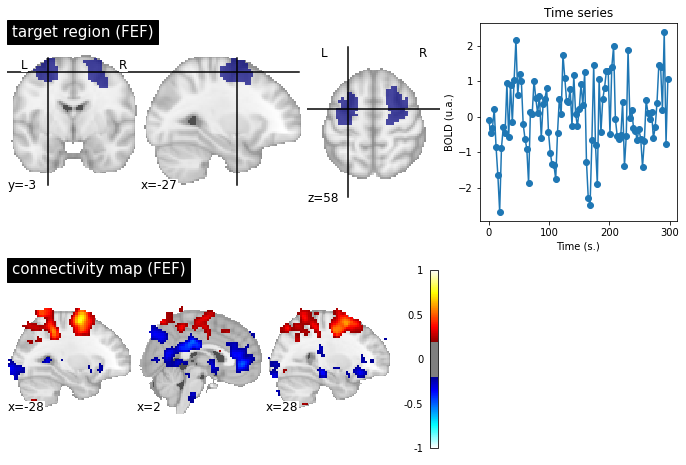
Fig. 86 A target region is selected at the "frontal eye field" (FEF) level, to generate a connectivity map on a participant from the ADHD-200 [Milham et al., 2012] dataset. The significance level is liberally selected (|r|>0.2). In addition to the dorsal attentional network associated with the FEF, the connectivity map highlights a negative correlation with the PCC and the anterior cingulate cortex (ACC). The ACC and PCC are key regions of the default mode network. This figure is generated by python code using the nilearn library (click on + to see the code), and is distributed under CC-BY license.

The default mode network is not the only one that can be identified at rest. We have already seen the sensorimotor network which was first identified by Biswal et al. [Biswal et al., 1995]. Another network commonly examined in the literature is the dorsal attentional network (DAN), which notably includes the superior intraparietal sulci (IPS) and the frontal eye fields (FEF). The DAN is often identified as activated in experiments using a cognitively demanding fMRI task, and is sometimes referred to as the "task positive network" - even though it is not positively engaged by all tasks. In 2005, Fox and colleagues [Fox et al., 2005] notice a negative correlation between DAN and the default mode network. This analysis reinforces the notion of spontaneous transitions between a mental state directed towards external stimuli, and an introspective state, reflecting the competition between two distributed networks.

Global signal regression controversies

The negative correlations of the Fig. 86 are strong only when we apply certain data denoising steps, and in particular the global signal regression. Significant controversy has arisen around the negative connections, as some researchers believe it to be an artifact related to this preprocessing step. Nevertheless, negative correlations can be observed robustly for participants who move very little, and whose signal is therefore particularly clean. Their amplitude is however low in the absence of regression of the overall signal.

Intrinsic vs Extrinsic Activity

Resting networks can be observed even in the presence of a task. Rather than opposing the notion of rest and task, it is common to speak of intrinsic and extrinsic activity. Extrinsic activity is the activity evoked by a task, and reflects how the environment influences brain activity. In contrast, intrinsic activity refers to brain activity that emerges spontaneously, and is independent of external stimuli. Both types of activity are always present, and can interact with each other.

Functional networks

# Import libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from nilearn import datasets
from nilearn.image import math_img
from nilearn import image
from nilearn import masking
from nilearn.glm.first_level import FirstLevelModel
from nilearn import input_data
from nilearn.input_data import NiftiLabelsMasker
from nilearn.input_data import NiftiMasker
from nilearn import plotting

# Initialize the figure
fig = plt.figure(figsize=(12, 5), dpi=300)

# Import data
basc = datasets.fetch_atlas_basc_multiscale_2015() # the BASC multiscale atlas
adhd = datasets.fetch_adhd(n_subjects=10)          # ADHD200 preprocessed data (Athena pipeline)\

# Pre-processing parameters
num_data = 1
fwhm = 8
high_pass = 0.01
high_variance_confounds = False
time_samp = range(0, 100)

# Extract the signal for a functional atlas (BASC)
masker = input_data.NiftiLabelsMasker(
                                      basc['scale122'],
                                      resampling_target="data",
                                      high_pass=high_pass,
                                      t_r=3,
                                      high_variance_confounds=high_variance_confounds,
                                      standardize=True,
                                      memory='nilearn_cache',
                                      memory_level=1,
                                      smoothing_fwhm=fwhm).fit()
tseries = masker.transform(adhd.func[num_data])
print(f"Time series with shape {tseries.shape} (# time points, # parcels))")


# Applies global signal correction
from nilearn.signal import clean as signal_clean
gb_signal = signal_clean(
                        tseries.mean(axis=1).reshape([tseries.shape[0], 1]),
                        high_pass=high_pass,
                        t_r=3,
                        standardize=True)
tseries = masker.transform(adhd.func[num_data], confounds=gb_signal)

# Affiche le template
ax_plot = plt.subplot2grid((2, 4), (0, 0), colspan=2)
plotting.plot_roi(basc['scale122'], title="parcellation", axes=ax_plot, colorbar=True, cmap="viridis")

# We generate a connectome
from nilearn.connectome import ConnectivityMeasure
conn = np.squeeze(ConnectivityMeasure(kind='correlation').fit_transform([tseries]))

# we use scipy's hierarchical clustering implementation
from scipy.cluster.hierarchy import dendrogram, linkage, cut_tree
# That's the hierarchical clustering step
hier = linkage(conn, method='average', metric='euclidean') # scipy's hierarchical clustering
# HAC proceeds by iteratively merging brain regions, which can be visualized with a tree
res = dendrogram(hier, get_leaves=True, no_plot=True) # Generate a dendrogram from the hierarchy
order = res.get('leaves') # Extract the order on parcels from the dendrogram
part = np.squeeze(cut_tree(hier, n_clusters=10))

# Show the connectome
ax_plot = plt.subplot2grid((2, 4), (0, 2), rowspan=2, colspan=2)
ax_plot.set_xlabel('regions')
ax_plot.set_title('connectome')
pos = ax_plot.imshow(conn[order, :][:, order], cmap='magma', interpolation='nearest')
fig.colorbar(pos, ax=ax_plot)

# Show networks
ax_plot = plt.subplot2grid((2, 4), (1, 0), colspan=2)
part_img = masker.inverse_transform(part.reshape([1, 122]) + 1) # note the sneaky shift to 1-indexing
plotting.plot_roi(part_img,
                  title="regions",
                  colorbar=True,
                  cmap="inferno",
                  axes=ax_plot,
                  cut_coords=[0, -52, 26])

# Glue the figure
from myst_nb import glue
glue("network-fig", fig, display=False)

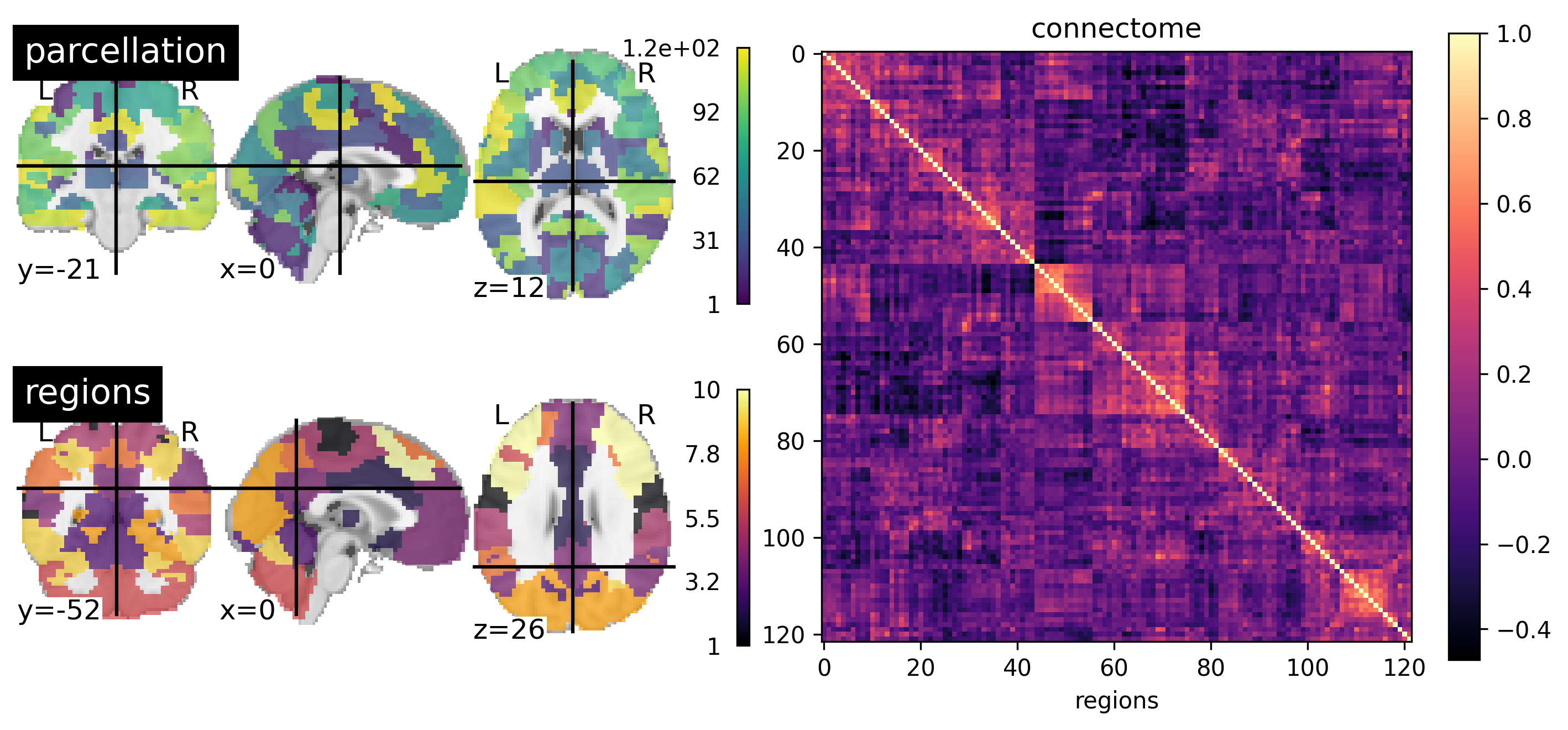
Fig. 87 A functional brain parcellation with 122 parcels is shown on the left (BASC). In the center, we see a matrix where each element represents the correlation between the activity of two regions. The plots have been ordered in such a way as to highlight diagonal squares: these are groups of regions whose activity correlates strongly with each other, and little with the rest of the brain. Clustering-type algorithms make it possible to automatically detect these groups of regions, called functional networks. An example of functional networks generated with hierarchical clustering is shown on the right, which notably identifies the default mode network. This figure is generated by python code using the nilearn library (click on + to see the code), and is distributed under CC-BY license.

In the last section, we spoke several times about working network, but without really defining what it is. When using a connectivity map, the functional network is the set of regions that appear in the map, and which are therefore connected to our target region. But this approach depends on the target region. Still, it’s intuitive that all connectivity maps using targets in, say, the default mode are going to look the same. To formalize this intuition, we need to introduce the notion of functional connectome.

A functional connectome is a matrix that represents all the (functional) connections of the brain. We therefore start by selecting a cerebral parcellation, then we calculate the correlation of the temporal activity for all the pairs of parcels in the brain. This correlation matrix is of size #plots x #plots. By using unsupervised learning techniques, such as clustering, it is possible to identify groups of regions that are strongly connected to each other, and weakly connected to the rest of the brain. This is the most common definition of a functional network. This type of approach makes it possible to divide the brain into networks, automatically and guided by data.

# Ignore warnings
import warnings
warnings.filterwarnings("ignore")

# Download data
from nilearn import datasets # Fetch data using nilearn
atlas_yeo = datasets.fetch_atlas_yeo_2011()        # the Yeo-Krienen atlas

# Initialize the figure
fig = plt.figure(figsize=(24, 16), dpi=300)

# Let's plot the Yeo-Krienen 7 clusters parcellation
from nilearn import plotting
from nilearn.image import math_img
import matplotlib.pyplot as plt
ax_plot = plt.subplot(4, 2, 1)
plotting.plot_roi(atlas_yeo.thick_7, title='Yeo-Krienen atlas-7',
                  colorbar=True, cmap='Paired', axes=ax_plot)

ax_plot = plt.subplot(4, 2, 2)
plotting.plot_roi(math_img('(img==1).astype(\'float\')', img=atlas_yeo.thick_7), title='Visual',
                  colorbar=True, cmap='Paired', axes=ax_plot, vmin=1, vmax=7)

ax_plot = plt.subplot(4, 2, 3)
plotting.plot_roi(math_img('2 * (img==2).astype(\'float\')', img=atlas_yeo.thick_7), title='Sensorimotor',
                  colorbar=True, cmap='Paired', axes=ax_plot, vmin=1, vmax=7)

ax_plot = plt.subplot(4, 2, 4)
plotting.plot_roi(math_img('3 * (img==3).astype(\'float\')', img=atlas_yeo.thick_7), title='Dorsal attention',
                  cut_coords=(-27, -5, 58), colorbar=True, cmap='Paired', axes=ax_plot, vmin=1, vmax=7)

ax_plot = plt.subplot(4, 2, 5)
plotting.plot_roi(math_img('4 * (img==4).astype(\'float\')', img=atlas_yeo.thick_7), title='Ventral attention / salience',
                  cut_coords=(-3, 19, 24), colorbar=True, cmap='Paired', axes=ax_plot, vmin=1, vmax=7)

ax_plot = plt.subplot(4, 2, 6)
plotting.plot_roi(math_img('5 * (img==5).astype(\'float\')', img=atlas_yeo.thick_7), title='mesolimbique',
                  colorbar=True, cmap='Paired', axes=ax_plot, vmin=1, vmax=7)

ax_plot = plt.subplot(4, 2, 7)
plotting.plot_roi(math_img('6 * (img==6).astype(\'float\')', img=atlas_yeo.thick_7), title='fronto-parietal',
                  colorbar=True, cmap='Paired', axes=ax_plot, vmin=1, vmax=7)

ax_plot = plt.subplot(4, 2, 8)
plotting.plot_roi(math_img('7 * (img==7).astype(\'float\')', img=atlas_yeo.thick_7), title='Default mode',
                  colorbar=True, cmap='Paired', axes=ax_plot, vmin=1, vmax=7)

# Glue the figure
from myst_nb import glue
glue("yeo-krienen-fig", fig, display=False)

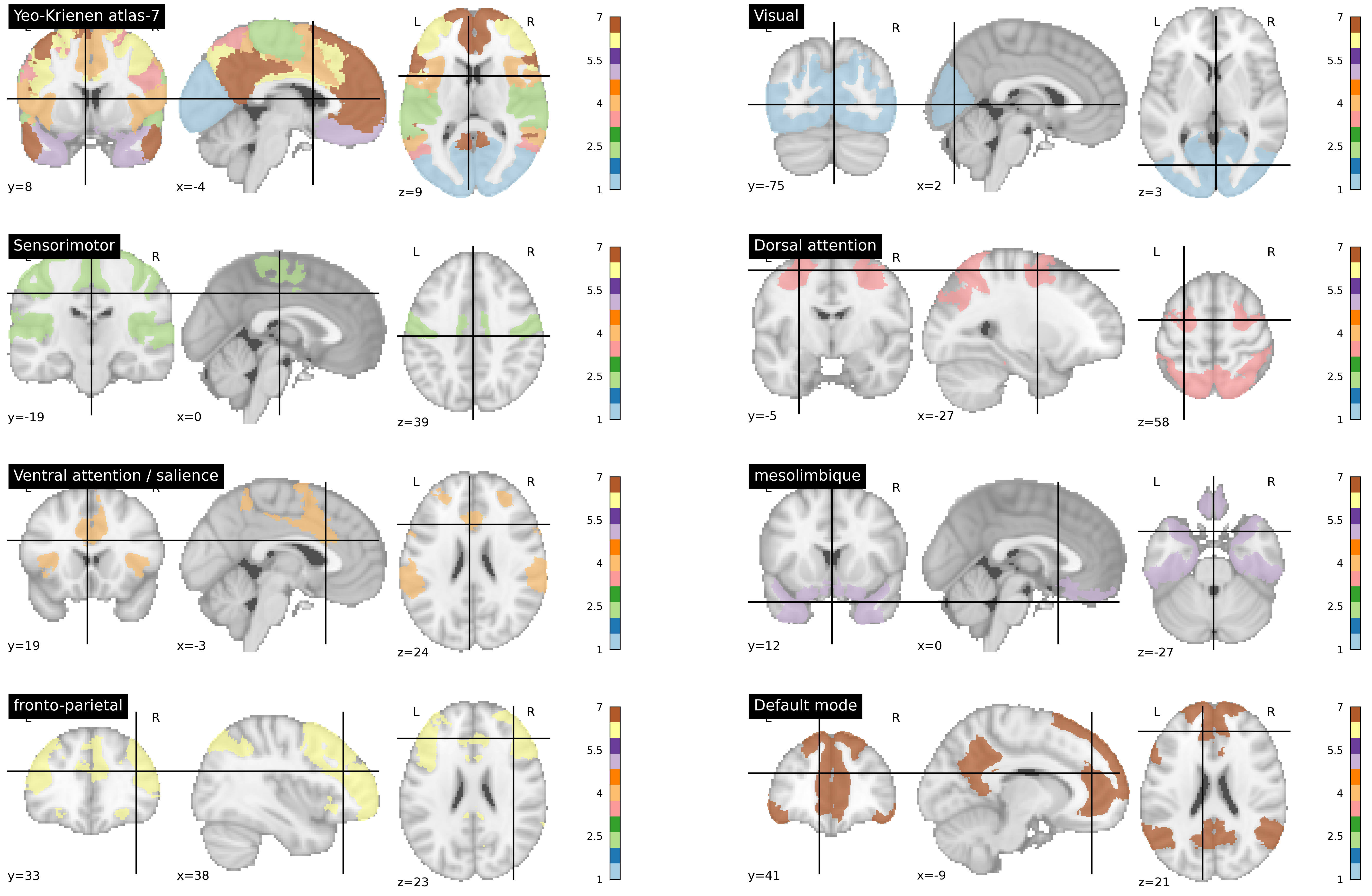
Fig. 88 Atlas of Yeo-Krienen [Thomas Yeo et al., 2011] constructed by clustering analysis from resting state fMRI data from a large number of participants. The networks are defined at several resolutions in this atlas (7 and 17). Here, the division into 7 large distributed networks is presented. This figure is generated by python code using the nilearn library (click on + to see the code), and is distributed under CC-BY license.

There is not an exact number of brain networks, but rather a hierarchy of more or less specialized networks. Nevertheless, many articles have studied a division into 7 cortical networks. The atlas by Yeo, Krienen and colleagues [Thomas Yeo et al., 2011] is widely used, and identifies seven major networks. Some of these networks have already been discussed in this chapter: default mode, dorsal attentional, sensorimotor. Two other associative networks must be added: the frontoparietal and the ventral attentional (sometimes called salience). There is also a visual network, and a mesolimbic network involving the temporal pole and the orbitofrontal cortex. Note that this atlas ignores all subcortical structures. The same study proposed a division into 17 sub-networks. You can use this interactive tool to explore the multiscale organization of functional networks interactively, using the MIST atlas { quote:p}urchs_mist_2019.

Conclusions

• Functional connectivity consists of measuring the coherence (correlation) between the activity of two regions (or voxels) of the brain.

• A functional connectivity map makes it possible to study the connectivity between a target region and the rest of the brain.

• Functional connectivity can be observed at rest (spontaneous activity), in the absence of an experimental protocol. In general, there is a superposition of intrinsic activity (linked to spontaneous activity) and extrinsic (linked to the environment).

• Resting fMRI connectivity played a key role in the discovery of the default mode network.

• A functional network is a group of regions whose spontaneous activity shows strong intra-network functional connectivity, and weak connectivity with the rest of the brain. Different atlases of networks at rest exist, and at different scales.

References

BCCD+17

Pierre Bellec, Carlton Chu, François Chouinard-Decorte, Yassine Benhajali, Daniel S. Margulies, and R. Cameron Craddock. The Neuro Bureau ADHD-200 Preprocessed repository. NeuroImage, 144:275–286, January 2017. URL: https://www.sciencedirect.com/science/article/pii/S105381191630283X (visited on 2022-04-01), doi:10.1016/j.neuroimage.2016.06.034.

BZYHH95(1,2,3)

Bharat Biswal, F. Zerrin Yetkin, Victor M. Haughton, and James S. Hyde. Functional connectivity in the motor cortex of resting human brain using echo-planar mri. Magnetic Resonance in Medicine, 34(4):537–541, 1995. _eprint: https://onlinelibrary.wiley.com/doi/pdf/10.1002/mrm.1910340409. URL: https://onlinelibrary.wiley.com/doi/abs/10.1002/mrm.1910340409 (visited on 2022-04-25), doi:10.1002/mrm.1910340409.

BD19

Randy L. Buckner and Lauren M. DiNicola. The brain’s default network: updated anatomy, physiology and evolving insights. Nature Reviews Neuroscience, 20(10):593–608, October 2019. Number: 10 Publisher: Nature Publishing Group. URL: https://www.nature.com/articles/s41583-019-0212-7 (visited on 2022-04-25), doi:10.1038/s41583-019-0212-7.

FR07

Michael D. Fox and Marcus E. Raichle. Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nature Reviews Neuroscience, 8(9):700–711, September 2007. Number: 9 Publisher: Nature Publishing Group. URL: https://www.nature.com/articles/nrn2201 (visited on 2022-04-25), doi:10.1038/nrn2201.

FSV+05

Michael D. Fox, Abraham Z. Snyder, Justin L. Vincent, Maurizio Corbetta, David C. Van Essen, and Marcus E. Raichle. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proceedings of the National Academy of Sciences, 102(27):9673–9678, July 2005. Publisher: Proceedings of the National Academy of Sciences. URL: https://www.pnas.org/doi/abs/10.1073/pnas.0504136102 (visited on 2022-04-25), doi:10.1073/pnas.0504136102.

GKRM03(1,2)

Michael D. Greicius, Ben Krasnow, Allan L. Reiss, and Vinod Menon. Functional connectivity in the resting brain: A network analysis of the default mode hypothesis. Proceedings of the National Academy of Sciences, 100(1):253–258, January 2003. Publisher: Proceedings of the National Academy of Sciences. URL: https://www.pnas.org/doi/abs/10.1073/pnas.0135058100 (visited on 2022-04-25), doi:10.1073/pnas.0135058100.

MFMM12(1,2,3)

Michael Milham, Damien Fair, Maarten Mennes, and Stewart Mostofsky. The adhd-200 consortium: a model to advance the translational potential of neuroimaging in clinical neuroscience. Frontiers in Systems Neuroscience, 2012. URL: https://www.frontiersin.org/article/10.3389/fnsys.2012.00062 (visited on 2022-04-01).

RMS+01

Marcus E. Raichle, Ann Mary MacLeod, Abraham Z. Snyder, William J. Powers, Debra A. Gusnard, and Gordon L. Shulman. A default mode of brain function. Proceedings of the National Academy of Sciences, 98(2):676–682, January 2001. Publisher: Proceedings of the National Academy of Sciences. URL: https://www.pnas.org/doi/full/10.1073/pnas.98.2.676 (visited on 2022-04-25), doi:10.1073/pnas.98.2.676.

SL08

Amir Shmuel and David A. Leopold. Neuronal correlates of spontaneous fluctuations in fMRI signals in monkey visual cortex: Implications for functional connectivity at rest. Human Brain Mapping, 29(7):751–761, 2008. _eprint: https://onlinelibrary.wiley.com/doi/pdf/10.1002/hbm.20580. URL: https://onlinelibrary.wiley.com/doi/abs/10.1002/hbm.20580 (visited on 2022-04-25), doi:10.1002/hbm.20580.

SCB+97

Gordon L. Shulman, Maurizio Corbetta, Randy L. Buckner, Julie A. Fiez, Francis M. Miezin, Marcus E. Raichle, and Steven E. Petersen. Common Blood Flow Changes across Visual Tasks: I. Increases in Subcortical Structures and Cerebellum but Not in Nonvisual Cortex. Journal of Cognitive Neuroscience, 9(5):624–647, October 1997. URL: https://doi.org/10.1162/jocn.1997.9.5.624 (visited on 2022-04-25), doi:10.1162/jocn.1997.9.5.624.

TYKS+11(1,2)

B. T. Thomas Yeo, Fenna M. Krienen, Jorge Sepulcre, Mert R. Sabuncu, Danial Lashkari, Marisa Hollinshead, Joshua L. Roffman, Jordan W. Smoller, Lilla Zöllei, Jonathan R. Polimeni, Bruce Fischl, Hesheng Liu, and Randy L. Buckner. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. Journal of Neurophysiology, 106(3):1125–1165, September 2011. Publisher: American Physiological Society. URL: https://journals.physiology.org/doi/full/10.1152/jn.00338.2011 (visited on 2022-04-26), doi:10.1152/jn.00338.2011.

Exercices

In the following we created a few exercises that aim to recap core aspects of this part of the course and thus should allow you to assess if you understood the main points.

We start with the following “resting-state network” video:

from IPython.display import HTML
import warnings
warnings.filterwarnings("ignore")

# Youtube
HTML('<iframe width="560" height="315" src="https://www.youtube.com/embed/_Iph3WW9UOU?start=18" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>')

Exercice 5.1.

“The Seventh Day” (sic), excerpt in French: 0:54 - 4:35

1. Who represents the young man?

2. What result does it refer to?

3. Who represents the young woman?

4. What outcome does it refer to?

5. Why call this film “the seventh day” (sic)?

Exercice 5.2.

“Neuro-meteorology”: 4:48 - 5:30

1. What networks are we talking about here?

2. Why does he refer to the default mode network and the “task-positive” network as “Yin and yang”?

3. Are any networks missing in this forecast?

4. Why is turbulence in the precuneus (or rather the posterior cingulate cortex) interesting?

Exercice 5.3.

“Hardball”: 8:01 - 9:46

1. Is it true that spontaneous activity is present both at rest and during a task?

2. Is it true that spontaneous activity has mainly been studied in a resting state in fMRI?

3. How is it “unpsychological” to study a condition of rest?

4. Open question: is one of them right? Or both?

Exercice 5.4.

Connectivity map: true/false

1. A connectivity map changes if the target region is changed.

2. To define a target region, one must generate an activation map.

3. A functional connectivity map has values between 0 and 1.

4. An fMRI connectivity map is a tool to identify the default mode network.

Exercice 5.5.

Spontaneous and evoked activity: true/false

1. Spontaneous brain activity occurs only in a state of rest.

2. Brain activity evoked by a task can be characterized by an fMRI activation map.

3. Spontaneous brain activity is greater at rest than during a visual task in certain parts of the brain.

Exercice 5.6.

Working networks: true/false

1. There are exactly 7 functional networks in the brain.

2. A functional network is composed of regions with strong functional connectivity.

3. The default mode network can be identified with an activation map.

4. Default mode network regions are negatively correlated with sensorimotor network regions.

Exercice 5.7

To answer this question, read the article by Shukla et al, “Aberrant Frontostriatal Connectivity in Negative Symptoms of Schizophrenia”, published in Schizophrenia Bulletin (2019, 45(5): 1051-59) and available open access at this address. The following questions require short answers.

• What software was used to analyze the fMRI data?

• What experimental condition was used during the fMRI acquisitions?

• What was the spatial smoothing setting?

• Has the data been motion corrected? Why?

• Did one of the two groups move more than the other?

• What filtering and noise correction procedures have been applied?

• In which stereotactic space are group analyzes performed?

• What type of connectivity metric is used in the article?

Exercice 5.8.

We want to compare the functional connectivity between young and old people. Name three potential confounders, which are not related to intrinsic neural activity.

previous

Nilearn GLM: statistical analyses of MRI in Python

next

Functional connectivity and resting state